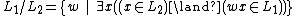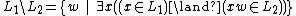“Quotient of a formal language”的意思、由来-开放百科全书

词条

Quotient of a formal language

释义

Example
Properties
See also
References

In mathematics and computer science, the right quotient (or simply quotient) of a formal language with a formal language is the language consisting of strings w such that wx is in for some string x in .^[1] In symbols, we write:

In other words, each string in 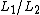is the prefix of a s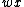tring in , with the remainder of the word being a string in .

Similarly, the left quotient of with is the language consisting of strings w such that xw is in for some string x in . In symbols, we write:

The left quotient can be regarded as the set of postfixes that complete words from , such that the resulting word is in .

Example

Consider

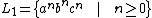
and

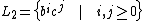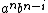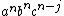Now, if we insert a divider into the middle of an element of , the part on the right is in only if the divider is placed adjacent to a b (in which case i ≤ n and j = n) or adjacent to a c (in which case i = 0 and j ≤ n). The part on the left, therefore, will be either or ; and 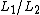can be written as

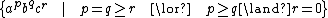Properties

Some common closure properties of the right quotient include:

The quotient of a regular language with any other language is regular.
The quotient of a context free language with a regular language is context free.
The quotient of two context free languages can be any recursively enumerable language.
The quotient of two recursively enumerable languages is recursively enumerable.

These closure properties hold for both left and right quotients.

References

1. ^{{cite book|last1=Linz|first1=Peter|title=An Introduction to Formal Languages and Automata|date=2011|publisher=Jones & Bartlett Publishers|isbn=9781449615529|pages=104-108|url=https://books.google.com/books?id=hsxDiWvVdBcC&pg=PA104&dq=right+quotient+automata&hl=en&sa=X&ei=N-C6U4DVIuKrigKztIC4Dw&ved=0CBwQ6AEwAA#v=onepage&q=right%20quotient%20automata&f=false|accessdate=7 July 2014}}

1 : Formal languages

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Example

Properties

See also

References