- The metric
- Charged black holes
- Gravitational time dilation
- Christoffel symbols
- Equations of motion
- Alternative formulation of metric
- See also
- Notes
- References
- External links
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M.
The metric was discovered by Hans Reissner,[1] Hermann Weyl,[2] Gunnar Nordström[3] and George Barker Jeffery.[4]
The metric
In spherical coordinates 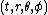 , the Reissner–Nordström metric (aka the line element) is
, the Reissner–Nordström metric (aka the line element) is
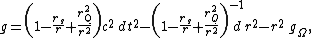 }}
}}where  is the speed of light,
is the speed of light,  is the time coordinate (measured by a stationary clock at infinity),
is the time coordinate (measured by a stationary clock at infinity),  is the radial coordinate, and
is the radial coordinate, and 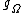 is the standard metric on the unit radius 2-sphere which if coordinatised by
is the standard metric on the unit radius 2-sphere which if coordinatised by 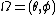 reads
reads
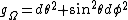 }}
}} is the Schwarzschild radius of the body given by
is the Schwarzschild radius of the body given by
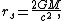 }}
}}and  is a characteristic length scale given by
is a characteristic length scale given by
 }}
}}Here 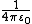 is Coulomb force constant
is Coulomb force constant  .
.
The total mass of the central body and its irreducible mass are related by[5][6]
{{block indent|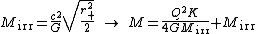 .}}
.}}The difference between  and
and 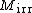 is due to the equivalence of mass and energy, which makes the electric field energy also contribute to the total mass.
is due to the equivalence of mass and energy, which makes the electric field energy also contribute to the total mass.
In the limit that the charge  (or equivalently, the length-scale
(or equivalently, the length-scale  ) goes to zero, one recovers the Schwarzschild metric. The classical Newtonian theory of gravity may then be recovered in the limit as the ratio
) goes to zero, one recovers the Schwarzschild metric. The classical Newtonian theory of gravity may then be recovered in the limit as the ratio 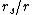 goes to zero. In the limit that both
goes to zero. In the limit that both 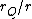 and
and 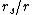 go to zero, the metric becomes the Minkowski metric for special relativity.
go to zero, the metric becomes the Minkowski metric for special relativity.
In practice, the ratio 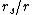 is often extremely small. For example, the Schwarzschild radius of the Earth is roughly 9 mm (3/8 inch), whereas a satellite in a geosynchronous orbit has a radius
is often extremely small. For example, the Schwarzschild radius of the Earth is roughly 9 mm (3/8 inch), whereas a satellite in a geosynchronous orbit has a radius  that is roughly four billion times larger, at 42,164 km (26,200 miles). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black holes and other ultra-dense objects such as neutron stars.
that is roughly four billion times larger, at 42,164 km (26,200 miles). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black holes and other ultra-dense objects such as neutron stars.
Charged black holes
Although charged black holes with rQ ≪ rs are similar to the Schwarzschild black hole, they have two horizons: the event horizon and an internal Cauchy horizon.[7] As with the Schwarzschild metric, the event horizons for the spacetime are located where the metric component grr diverges; that is, where
{{block indent|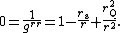 }}
}}This equation has two solutions:
{{block indent|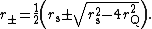 }}
}}These concentric event horizons become degenerate for 2rQ = rs, which corresponds to an extremal black hole. Black holes with 2rQ > rs can not exist in nature because if the charge is greater than the mass there can be no physical event horizon[8] (the term under the square root becomes negative). Objects with a charge greater than their mass can exist in nature, but they can not collapse down to a black hole, and if they could, they would display a naked singularity.[9] Theories with supersymmetry usually guarantee that such "superextremal" black holes cannot exist.
The electromagnetic potential is
{{block indent|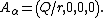 }}
}}If magnetic monopoles are included in the theory, then a generalization to include magnetic charge P is obtained by replacing Q2 by Q2 + P2 in the metric and including the term Pcos θ dφ in the electromagnetic potential.{{clarify|date=January 2013}}
Gravitational time dilation
The gravitational time dilation in the vicinity of the central body is given by
{{block indent|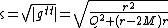 }}
}}which relates to the local radial escape-velocity of a neutral particle
{{block indent|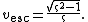 }}
}}Christoffel symbols
The Christoffel symbols
{{block indent|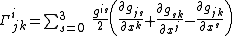 }}
}}with the indices
{{block indent| }}
}}give the nonvanishing expressions
{{block indent|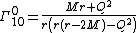 }}{{block indent|
}}{{block indent|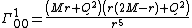 }}{{block indent|
}}{{block indent|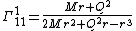 }}{{block indent|
}}{{block indent|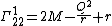 }}{{block indent|
}}{{block indent|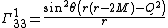 }}{{block indent|
}}{{block indent|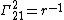 }}{{block indent|
}}{{block indent|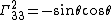 }}{{block indent|
}}{{block indent|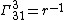 }}{{block indent|
}}{{block indent|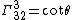 }}
}}Given the Christoffel symbols, one can compute the geodesics of a test-particle.[10][11]
Equations of motion
Because of the spherical symmetry of the metric, the coordinate system can always be aligned in a way that the motion of a test-particle is confined to a plane, so for brevity and without restriction of generality we further use Ω instead of θ and φ. In dimensionless natural units of G = M = c = K = 1 the motion of an electrically charged particle with the charge q is given by
{{block indent|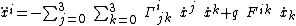 }}
}}which gives
{{block indent|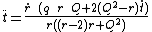 }}{{block indent|
}}{{block indent|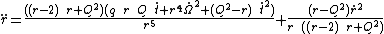 }}{{block indent|
}}{{block indent|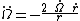 }}
}}The total time dilation between the test-particle and an observer at infinity is
{{block indent|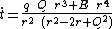 }}
}}The first derivatives 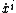 and the contravariant components of the local 3-velocity
and the contravariant components of the local 3-velocity 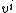 are related by
are related by
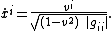 }}
}}which gives the initial conditions
{{block indent|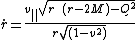 }}{{block indent|
}}{{block indent|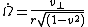 }}
}}The specific orbital energy
{{block indent|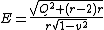 }}
}}and the specific relative angular momentum
{{block indent|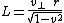 }}
}}of the test-particle are conserved quantities of motion.  and
and  are the radial and transverse components of the local velocity-vector. The local velocity is therefore
are the radial and transverse components of the local velocity-vector. The local velocity is therefore
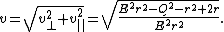 }}
}}Alternative formulation of metric
The metric can alternatively be expressed like this:
{{block indent|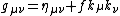 }}{{block indent|
}}{{block indent|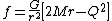 }}{{block indent|
}}{{block indent| }}{{block indent|
}}{{block indent|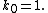 }}
}}Notice that k is a unit vector. Here M is the constant mass of the object, Q is the constant charge of the object, and η is the Minkowski tensor.
See also
- Black hole electron
Notes
2. ^{{cite journal | last=Weyl | first=H. | date=1917 | title=Zur Gravitationstheorie | journal=Annalen der Physik | volume=54 | pages=117–145 | doi=10.1002/andp.19173591804 | language=German| bibcode=1917AnP...359..117W }}
3. ^{{cite journal | last=Nordström | first=G. | date=1918 | title=On the Energy of the Gravitational Field in Einstein's Theory | journal=Verhandl. Koninkl. Ned. Akad. Wetenschap., Afdel. Natuurk., Amsterdam | volume=26 | pages=1201–1208}}
4. ^{{cite journal | last=Jeffery | first=G. B. | date=1921 | title=The field of an electron on Einstein’s theory of gravitation | journal=Proc. Roy. Soc. Lond. A | volume=99 | pages=123–134 | doi=10.1098/rspa.1921.0028 | bibcode=1921RSPSA..99..123J }}
5. ^Thibault Damour: Black Holes: Energetics and Thermodynamics, S. 11 ff.
6. ^Ashgar Quadir: The Reissner Nordström Repulsion
7. ^{{cite book |last=Chandrasekhar |first=S. |authorlink=Subrahmanyan Chandrasekhar |title=The Mathematical Theory of Black Holes |date=1998 |publisher=Oxford University Press |isbn=0-19850370-9 |edition=Reprinted |url=http://www.oup.com/us/catalog/general/subject/Physics/Relativity/?view=usa&ci=9780198503705 |accessdate=13 May 2013 |page=205 |quote=And finally, the fact that the Reissner–Nordström solution has two horizons, an external event horizon and an internal 'Cauchy horizon,' provides a convenient bridge to the study of the Kerr solution in the subsequent chapters. |deadurl=yes |archiveurl=https://web.archive.org/web/20130429125834/http://www.oup.com/us/catalog/general/subject/Physics/Relativity/?view=usa |archivedate=29 April 2013 |df= }}
8. ^Andrew Hamilton: The Reissner Nordström Geometry {{webarchive|url=https://web.archive.org/web/20070707053358/http://casa.colorado.edu/~ajsh/rn.html |date=2007-07-07 }} (Casa Colorado)
9. ^Carter, Brandon. Global Structure of the Kerr Family of Gravitational Fields, Physical Review, page 174
10. ^Leonard Susskind: The Theoretical Minimum: Geodesics and Gravity, (General Relativity Lecture 4, timestamp: [https://www.youtube.com/watch?v=YdnLcYNdTzE&t=34m18s&index=4&list=PL9peWTxCcrBLLE89-Pwab3Qc1uoaKEH0e 34m18s])
11. ^Eva Hackmann, Hongxiao Xu: [https://arxiv.org/pdf/1304.2142.pdf#page=4 Charged particle motion in Kerr–Newmann space-times]
References
- {{cite book | last1=Adler | first1=R. | last2=Bazin | first2=M. | last3=Schiffer | first3=M. | date=1965 | title=Introduction to General Relativity | publisher=McGraw-Hill Book Company | location=New York | isbn=978-0-07-000420-7 | pages=395–401}}
- {{cite book |last=Wald |first=Robert M. |authorlink=Robert Wald |date=1984 |title=General Relativity |publisher=The University of Chicago Press |location=Chicago |isbn=978-0-226-87032-8 |pages=158, 312–324 |url=http://press.uchicago.edu/ucp/books/book/chicago/G/bo5952261.html |accessdate=27 April 2013}}
External links
- [https://web.archive.org/web/20070707053358/http://casa.colorado.edu/~ajsh/rn.html spacetime diagrams] including Finkelstein diagram and Penrose diagram, by Andrew J. S. Hamilton
- "Particle Moving Around Two Extreme Black Holes" by Enrique Zeleny, The Wolfram Demonstrations Project.
- John Vergiels
- John Verhoogen
- John Verity (judge)
- John Verity (lawyer)
- John Vernil Lopez
- John Vernon (cricketer)
- John Vernon Harrison
- John Vernon Pettigrew
- John Vernon Rob
- John Vernon Trathen
- John Vernou Bouvier Jr.
- John Veryard
- John Vesey (1638-1716)
- John Vesey, 1st Baron Knapton
- John Vesey, 2nd Viscount de Vesci
- John Vesey, 4th Viscount de Vesci
- John Vesser
- John V Evans(astronomer)
- John V. Evans (astronomer)
- Johnvic De Guzman
- John Vic De Guzman
- John Victor
- John Victor Morais
- John Victor Nash
- John Victor Saunders