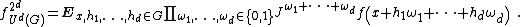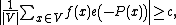- Definition
- Inverse conjectures
- References
In mathematics, in the field of additive combinatorics, a Gowers norm or uniformity norm is a class of norm on functions on a finite group or group-like object which are used in the study of arithmetic progressions in the group. It is named after Timothy Gowers, who introduced it in his work on Szemerédi's theorem.[1]
Definition
Let f be a complex-valued function on a finite Abelian group G and let J denote complex conjugation. The Gowers d-norm is
Gowers norms are also defined for complex valued functions f on a segment [N]={0,1,2,...,N-1}, where N is a positive integer. In this context, the uniformity norm is given as 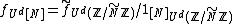 , where
, where  is a large integer,
is a large integer,  denotes the indicator function of [N], and
denotes the indicator function of [N], and 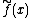 is equal to
is equal to  for
for 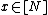 and
and  for all other
for all other  . This definition does not depend on
. This definition does not depend on  , as long as
, as long as 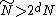 .
.
Inverse conjectures
An inverse conjecture for these norms is a statement asserting that if a bounded function f has a large Gowers d-norm then f correlates with a polynomial phase of degree d-1 or other object with polynomial behaviour (e.g. a (d-1)-step nilsequence). The precise statement depends on the Gowers norm under consideration.
The Inverse Conjecture for vector spaces over a finite field 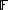 asserts that for any
asserts that for any  there exists a constant
there exists a constant  such that for any finite dimensional vector space V over
such that for any finite dimensional vector space V over 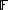 and any complex valued function
and any complex valued function  on
on  , bounded by 1, such that
, bounded by 1, such that  , there exists a polynomial sequence
, there exists a polynomial sequence  such that
such that
where 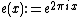 . This conjecture was proved to be true by Bergelson, Tao, and Ziegler.[2][3][4]
. This conjecture was proved to be true by Bergelson, Tao, and Ziegler.[2][3][4]
The Inverse Conjecture for Gowers  norm asserts that for any
norm asserts that for any  , a finite collection of (d-1)-step nilmanifolds
, a finite collection of (d-1)-step nilmanifolds 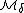 and constants
and constants 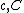 can be found, so that the following is true. If
can be found, so that the following is true. If  is a positive integer and
is a positive integer and 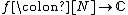 is bounded in absolute value by 1 and
is bounded in absolute value by 1 and 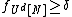 , then there exists a nilmanifold
, then there exists a nilmanifold 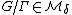 and a nilsequence
and a nilsequence  where
where 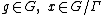 and
and 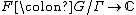 bounded by 1 in absolute value and with Lipschitz constant bounded by
bounded by 1 in absolute value and with Lipschitz constant bounded by  such that:
such that:
This conjecture was proved to be true by Green, Tao, and Ziegler.[5][6] It should be stressed that the appearance of nilsequences in the above statement is necessary. The statement is no longer true if we only consider polynomial phases.
References
2. ^{{cite journal | last1=Bergelson | first1=Vitaly | last2=Tao | first2=Terence | author2-link = Terence Tao | last3=Ziegler | first3=Tamar | author3-link = Tamar Ziegler | title=An inverse theorem for the uniformity seminorms associated with the action of
 | mr=2594614 | journal=Geom. Funct. Anal. | year=2010 | volume=19 | issue=6 | pages=1539–1596 | doi=10.1007/s00039-010-0051-1}}
| mr=2594614 | journal=Geom. Funct. Anal. | year=2010 | volume=19 | issue=6 | pages=1539–1596 | doi=10.1007/s00039-010-0051-1}}3. ^{{cite journal | last1=Tao | first1=Terence | author1-link = Terence Tao | last2=Ziegler | first2=Tamar | author2-link = Tamar Ziegler | title=The inverse conjecture for the Gowers norm over finite fields via the correspondence principle | year=2010 | journal=Analysis & PDE | volume=3 | issue=1 | pages=1–20 | doi=10.2140/apde.2010.3.1 | mr=2663409| arxiv=0810.5527 }}
4. ^{{cite journal| doi = 10.1007/s00026-011-0124-3| title = The Inverse Conjecture for the Gowers Norm over Finite Fields in Low Characteristic| journal = Annals of Combinatorics| volume = 16| pages = 121–188| year = 2011| last1 = Tao | first1 = Terence | author1-link = Terence Tao| last2 = Ziegler | first2 = Tamar | author2-link = Tamar Ziegler| mr = 2948765| arxiv = 1101.1469}}
5. ^{{cite journal | last1 = Green | first1 = Ben | author1-link = Ben Green (mathematician)| last2 = Tao | first2 = Terence | author2-link = Terence Tao| last3 = Ziegler | first3 = Tamar | author3-link = Tamar Ziegler| title = An inverse theorem for the Gowers
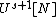 -norm| journal = Electron. Res. Announc. Math. Sci.| volume = 18| year = 2011| pages = 69–90| doi = 10.3934/era.2011.18.69| mr = 2817840| arxiv = 1006.0205}}
-norm| journal = Electron. Res. Announc. Math. Sci.| volume = 18| year = 2011| pages = 69–90| doi = 10.3934/era.2011.18.69| mr = 2817840| arxiv = 1006.0205}}6. ^{{cite journal| doi = 10.4007/annals.2012.176.2.11| title = An inverse theorem for the Gowers
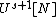 -norm| journal = Annals of Mathematics| volume = 176| issue = 2| pages = 1231–1372| year = 2012| last1 = Green | first1 = Ben | author1-link = Ben Green (mathematician)| last2 = Tao | first2 = Terence | author2-link = Terence Tao| last3 = Ziegler | first3 = Tamar | author3-link = Tamar Ziegler| mr = 2950773| arxiv = 1009.3998}}
-norm| journal = Annals of Mathematics| volume = 176| issue = 2| pages = 1231–1372| year = 2012| last1 = Green | first1 = Ben | author1-link = Ben Green (mathematician)| last2 = Tao | first2 = Terence | author2-link = Terence Tao| last3 = Ziegler | first3 = Tamar | author3-link = Tamar Ziegler| mr = 2950773| arxiv = 1009.3998}}- {{cite book | zbl=1277.11010 | last=Tao | first=Terence | authorlink=Terence Tao | title=Higher order Fourier analysis | series=Graduate Studies in Mathematics | volume=142 | location=Providence, RI | publisher=American Mathematical Society | year=2012 | isbn=978-0-8218-8986-2 | url=http://terrytao.wordpress.com/books/higher-order-fourier-analysis/ | mr=2931680 }}
- Nidal Malik Hasan
- Nidamangalam Junction railway station
- Nidamanoor Mandal
- Nidamanur, Prakasam
- Nidamanuru, Krishna
- Nidamanuru railway station
- Nidamarru mandal
- Nida Mumtaz
- Nida plateau
- Nida Qila Pishin
- Nida Rashid
- Nidaros domprosti
- Nidaros Hockey
- Nida's Plateau
- Nida Tufekci
- Nida Ustundag
- Nidavadole mandal
- Nidavardyapuram
- Nida Üstündağ
- NIDD
- Nid d'Aigle
- Nidd Aqueduct
- Nidda Station
- Nidd Bridge railway station
- Nidd (disambiguation)