020 勾股弦数
可作为一直角三角形三边长的三正整数。即商高数，简称勾股数。西方称毕达哥拉斯(Pythagoras)数组。二次不定方程x2+y2＝z2的每组正整数解都是勾股弦数。《周髀算经》载：商高给出了最基本的勾股弦数：3、4、5。公元3世纪刘徽在《九章算术注》中提出了一系列勾股弦数： 5,12,13; 7,24,25;8,15,17;20,21,29。并给出了勾股弦数的一般形式。清代数学家陈杰、罗士琳、黄宗宪也都给出了勾股弦数的一般表示。通常采用罗士琳法求之。即设m、n为任意两正整数(m>n)，则m2-n2、2mn、m2+n2为一组勾股弦数。
勾股弦数gouguxuan shu
直角三角形的三条边长的三个正整数. 我国古代算书 《周脾算经》(公元前1世纪)曾记载了3,4,5是一组勾股弦数，刘徽《九章算术》进一步指出下列几组勾股弦数： 5,12,13; 7,24,25; 8,15,17; 20,21,29等.
在国外，公元前2000年左右，巴比伦人已经发现了几组勾股弦数.在古希腊，毕达哥拉斯学派发现，当m是奇数时，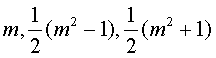
构成勾股弦数.
一般地说，不定方程x2+y2＝ z2的每一组正整数解就是一组勾股弦数. 怎样求出这个方程的全部正整数解？为此先对这个方程作一些简化. 设 (x,y)=d>1，则d2|x2+y2，即d2|z2，从而d|z，故原方程两边可约去d. 因此可以假定 (x,y)=1. 由此可知，x,y不能都是偶数，也不能都是奇数，否则x2+y2≡1+1≡2(mod4)，这时x2+y2不可能是平方数. 这样x,y必为一奇一偶.不妨假定x为偶数，有下述一般结果.不定方程
x2 +y2 = z2,(x,y)= 1,2|x, (1)
的一切正整数解可以用下述公式表出
x =2ab,y =a2 -b2 ,z =a2 +b2
其中 a> >6> 0,a,b一奇一偶，(a,b)= 1.由上述结果可以推出，单位圆周上的有理点有无穷多个（有理点是指两个坐标都是有理数的点），并且一切有理点可以表示成
