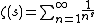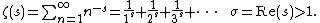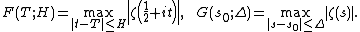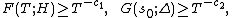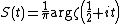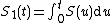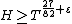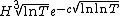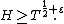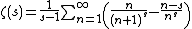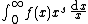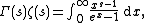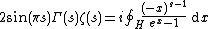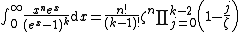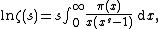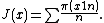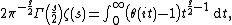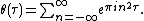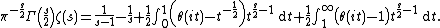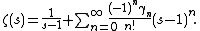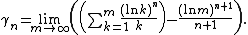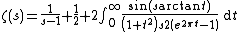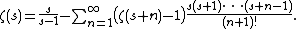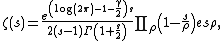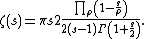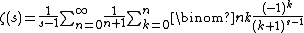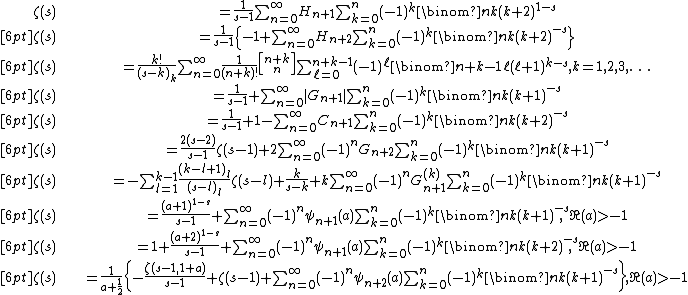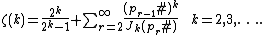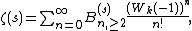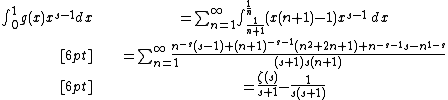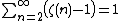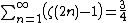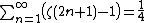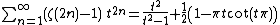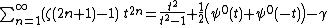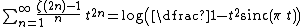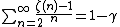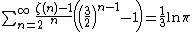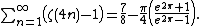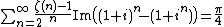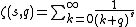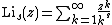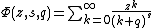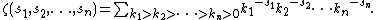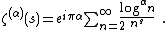- Definition
- Specific values
- Euler product formula
- Riemann's functional equation
- Zeros, the critical line, and the Riemann hypothesis The Hardy–Littlewood conjectures Zero-free region Other results
- Various properties Reciprocal Universality Estimates of the maximum of the modulus of the zeta function The argument of the Riemann zeta function
- Representations Dirichlet series Mellin-type integrals Theta functions Laurent series Integral Rising factorial Hadamard product Globally convergent series Series representation at positive integers via the primorial Series representation by the incomplete poly-Bernoulli numbers The Mellin transform of the Engel map
- Numerical algorithms
- Applications Infinite series
- Fractional derivative
- See also
- Notes
- References
- External links
| domain =
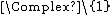
| codomain =

| image = File:Riemann-Zeta-Func.png
| caption = The Riemann zeta function {{math|ζ(z)}} plotted with domain coloring.[1]
| zero =
| plusinf =

| vr1 =

| f1 =
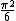
| vr2 =

| f2 =
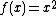
| vr3 =

| f3 =

}}
The Riemann zeta function or Euler–Riemann zeta function, {{math|ζ(s)}}, is a function of a complex variable s that analytically continues the sum of the Dirichlet series
which converges when the real part of {{mvar|s}} is greater than 1. More general representations of {{math|ζ(s)}} for all {{mvar|s}} are given below. The Riemann zeta function plays a pivotal role in analytic number theory and has applications in physics, probability theory, and applied statistics.
As a function of a real variable, Leonhard Euler first introduced and studied it in the first half of the eighteenth century without using complex analysis, which was not available at the time. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers.[2]
The values of the Riemann zeta function at even positive integers were computed by Euler. The first of them, {{math|ζ(2)}}, provides a solution to the Basel problem. In 1979 Apéry proved the irrationality of {{math|ζ(3)}}. The values at negative integer points, also found by Euler, are rational numbers and play an important role in the theory of modular forms. Many generalizations of the Riemann zeta function, such as Dirichlet series, Dirichlet {{mvar|L}}-functions and {{mvar|L}}-functions, are known.
Definition
The Riemann zeta function {{math|ζ(s)}} is a function of a complex variable {{math|s {{=}} σ + it}}. (The notation {{mvar|s}}, {{mvar|σ}}, and {{mvar|t}} is used traditionally in the study of the zeta function, following Riemann.)
The following infinite series converges for all complex numbers {{mvar|s}} with real part greater than 1, and defines {{math|ζ(s)}} in this case:
It can also be defined by the integral
The Riemann hypothesis is equivalent to the claim that this expression is valid when the real part of {{mvar|s}} is greater than {{sfrac|1|2}}.
Universality
The critical strip of the Riemann zeta function has the remarkable property of universality. This zeta-function universality states that there exists some location on the critical strip that approximates any holomorphic function arbitrarily well. Since holomorphic functions are very general, this property is quite remarkable. The first proof of universality was provided by Sergei Mikhailovitch Voronin in 1975.[13] More recent work has included effective versions of Voronin's theorem[14] and extending it to Dirichlet L-functions.[15][16]
Estimates of the maximum of the modulus of the zeta function
Let the functions {{math|F(T;H)}} and {{math|G(s0;Δ)}} be defined by the equalities
Here {{mvar|T}} is a sufficiently large positive number, {{math|0 < H ≪ ln ln T}}, {{math|s0 {{=}} σ0 + iT}}, {{math|{{sfrac|1|2}} ≤ σ0 ≤ 1}}, {{math|0 < Δ < {{sfrac|1|3}}}}. Estimating the values {{mvar|F}} and {{mvar|G}} from below shows, how large (in modulus) values {{math|ζ(s)}} can take on short intervals of the critical line or in small neighborhoods of points lying in the critical strip {{math|0 ≤ Re(s) ≤ 1}}.
The case {{math|H ≫ ln ln T}} was studied by Kanakanahalli Ramachandra; the case {{math|Δ > c}}, where {{math|c}} is a sufficiently large constant, is trivial.
Anatolii Karatsuba proved,[17][18] in particular, that if the values {{mvar|H}} and {{math|Δ}} exceed certain sufficiently small constants, then the estimates
hold, where {{math|c1}} and {{math|c2}} are certain absolute constants.
The argument of the Riemann zeta function
The function
is called the argument of the Riemann zeta function. Here {{math|arg ζ({{sfrac|1|2}} + it)}} is the increment of an arbitrary continuous branch of {{math|arg ζ(s)}} along the broken line joining the points {{math|2}}, {{math|2 + it}} and {{math|{{sfrac|1|2}} + it}}.
There are some theorems on properties of the function {{math|S(t)}}. Among those results[19][20] are the mean value theorems for {{math|S(t)}} and its first integral
on intervals of the real line, and also the theorem claiming that every interval {{math|(T, T + H]}} for
contains at least
points where the function {{math|S(t)}} changes sign. Earlier similar results were obtained by Atle Selberg for the case
Representations
Dirichlet series
An extension of the area of convergence can be obtained by rearranging the original series.[21] The series
converges for {{math|Re(s) > 0}}, while
converges even for {{math|Re(s) > −1}}. In this way, the area of convergence can be extended to {{math|Re(s) > −k}} for any negative integer {{math|−k}}.
Mellin-type integrals
{{unreferenced section|date=December 2014}}The Mellin transform of a function {{math|f(x)}} is defined as
in the region where the integral is defined. There are various expressions for the zeta-function as Mellin transform-like integrals. If the real part of {{mvar|s}} is greater than one, we have
where {{math|Γ}} denotes the gamma function. By modifying the contour, Riemann showed that
for all {{mvar|s}} (where {{mvar|H}} denotes the Hankel contour).
Starting with the integral formula 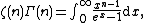 one can show[22] by substitution and iterated differentation for natural
one can show[22] by substitution and iterated differentation for natural 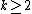
using the notation of umbral calculus where each power 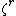 is to be replaced by
is to be replaced by 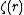 , so e.g. for
, so e.g. for  we have
we have 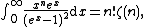 while for
while for  this becomes
this becomes
We can also find expressions which relate to prime numbers and the prime number theorem. If {{math|π(x)}} is the prime-counting function, then
for values with {{math|Re(s) > 1}}.
A similar Mellin transform involves the Riemann prime-counting function {{math|J(x)}}, which counts prime powers {{math|pn}} with a weight of {{math|{{sfrac|1|n}}}}, so that
Now we have
These expressions can be used to prove the prime number theorem by means of the inverse Mellin transform. Riemann's prime-counting function is easier to work with, and {{math|π(x)}} can be recovered from it by Möbius inversion.
Theta functions
The Riemann zeta function can be given by a Mellin transform[23]
in terms of Jacobi's theta function
However, this integral only converges if the real part of {{mvar|s}} is greater than 1, but it can be regularized. This gives the following expression for the zeta function, which is well defined for all {{mvar|s}} except 0 and 1:
Laurent series
{{unreferenced section|date=December 2014}}The Riemann zeta function is meromorphic with a single pole of order one at {{math|s {{=}} 1}}. It can therefore be expanded as a Laurent series about {{math|s {{=}} 1}}; the series development is then
The constants {{math|γn}} here are called the Stieltjes constants and can be defined by the limit
The constant term {{math|γ0}} is the Euler–Mascheroni constant.
Integral
For all {{math|s ∈ ℂ}}, {{math|s ≠ 1}} the integral relation (cf. Abel–Plana formula)
holds true, which may be used for a numerical evaluation of the zeta-function.
Rising factorial
Another series development using the rising factorial valid for the entire complex plane is{{Citation needed|date=October 2015}}
This can be used recursively to extend the Dirichlet series definition to all complex numbers.
The Riemann zeta function also appears in a form similar to the Mellin transform in an integral over the Gauss–Kuzmin–Wirsing operator acting on {{math|xs − 1}}; that context gives rise to a series expansion in terms of the falling factorial.[24]
Hadamard product
On the basis of Weierstrass's factorization theorem, Hadamard gave the infinite product expansion
where the product is over the non-trivial zeros {{mvar|ρ}} of {{math|ζ}} and the letter {{mvar|γ}} again denotes the Euler–Mascheroni constant. A simpler infinite product expansion is
This form clearly displays the simple pole at {{math|s {{=}} 1}}, the trivial zeros at −2, −4, … due to the gamma function term in the denominator, and the non-trivial zeros at {{math|s {{=}} ρ}}. (To ensure convergence in the latter formula, the product should be taken over "matching pairs" of zeros, i.e. the factors for a pair of zeros of the form {{mvar|ρ}} and {{math|1 − ρ}} should be combined.)
Globally convergent series
A globally convergent series for the zeta function, valid for all complex numbers {{mvar|s}} except {{math|s {{=}} 1 + {{sfrac|2πi|ln 2}}n}} for some integer {{mvar|n}}, was conjectured by Konrad Knopp[25] and proven by Helmut Hasse in 1930[26] (cf. Euler summation):
The series only appeared in an appendix to Hasse's paper, and did not become generally known until it was discussed by Jonathan Sondow in 1994.[25]
Hasse also proved the globally converging series
in the same publication,[26] but research by Iaroslav Blagouchine[26][27]
has found that this latter series was actually first published by Joseph Ser in 1926.[28] New proofs for both of these results were offered by Demetrios Kanoussis in 2017.[29] Other similar globally convergent series include
where {{math|Hn}} are the harmonic numbers, 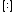 are the Stirling numbers of the first kind,
are the Stirling numbers of the first kind, 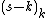 is the Pochhammer symbol, {{math|Gn}} are the Gregory coefficients, {{math|G{{su|b=n|p=(k)}}}} are the Gregory coefficients of higher order, {{math|Cn}} are the Cauchy numbers of the second kind ({{math|C1 {{=}} 1/2}}, {{math|C2 {{=}} 5/12}}, {{math|C3 {{=}} 3/8}},...), and {{math|ψn(a)}}
is the Pochhammer symbol, {{math|Gn}} are the Gregory coefficients, {{math|G{{su|b=n|p=(k)}}}} are the Gregory coefficients of higher order, {{math|Cn}} are the Cauchy numbers of the second kind ({{math|C1 {{=}} 1/2}}, {{math|C2 {{=}} 5/12}}, {{math|C3 {{=}} 3/8}},...), and {{math|ψn(a)}}
are the Bernoulli polynomials of the second kind, see Blagouchine's paper.[27]
Peter Borwein has developed an algorithm that applies Chebyshev polynomials to the Dirichlet eta function to produce a very rapidly convergent series suitable for high precision numerical calculations.[30]Series representation at positive integers via the primorial
Here {{math|pn#}} is the primorial sequence and {{math|Jk}} is Jordan's totient function.[31]
Series representation by the incomplete poly-Bernoulli numbers
The function {{mvar|ζ}} can be represented, for {{math|Re(s) > 1}}, by the infinite series
where {{math|k ∈ {−1, 0}|}}, {{math|Wk}} is the {{mvar|k}}th branch of the Lambert {{mvar|W}}-function, and {{math|B{{su|b=n, ≥2|p=(μ)}}}} is an incomplete poly-Bernoulli number.[32]
The Mellin transform of the Engel map
The function :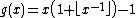 is iterated to find the coeffecients appearing in Engel expansions.
is iterated to find the coeffecients appearing in Engel expansions.
The Mellin transform of the map  is related to the Riemann zeta function by the formula
is related to the Riemann zeta function by the formula
Numerical algorithms
For 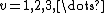 , the Riemann zeta function has for fixed
, the Riemann zeta function has for fixed 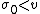 and for all
and for all 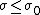 the following representation in terms of three absolutely and uniformly converging series,[33]
the following representation in terms of three absolutely and uniformly converging series,[33]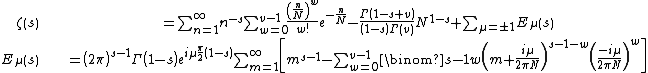 where for positive integer
where for positive integer 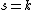 one has to take the limit value
one has to take the limit value 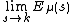 . The derivatives of
. The derivatives of 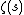 can be calculated by differentiating the above series termwise. From this follows an algorithm which allows to compute, to arbitrary precision,
can be calculated by differentiating the above series termwise. From this follows an algorithm which allows to compute, to arbitrary precision, 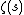 and its derivatives using at most
and its derivatives using at most 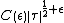 summands for any
summands for any 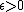 , with explicit error bounds. For
, with explicit error bounds. For 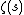 , these are as follows:
, these are as follows:
For a given argument  with
with 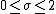 and
and 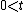 one can approximate
one can approximate 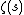 to any accuracy
to any accuracy 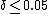 by summing the first series to
by summing the first series to 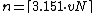 ,
, 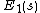 to
to 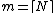 and neglecting
and neglecting 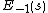 , if one chooses
, if one chooses  as the next higher integer of the unique solution of
as the next higher integer of the unique solution of 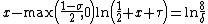 in the unknown
in the unknown  , and from this
, and from this 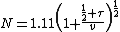 . For
. For 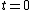 one can neglect
one can neglect 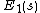 altogether. Under the mild condition
altogether. Under the mild condition 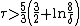 one needs at most
one needs at most 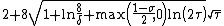 summands. Hence this algorithm is essentially as fast as the Riemann-Siegel formula. Similar algorithms are possible for Dirichlet L-functions.[33]
summands. Hence this algorithm is essentially as fast as the Riemann-Siegel formula. Similar algorithms are possible for Dirichlet L-functions.[33]
Applications
The zeta function occurs in applied statistics (see Zipf's law and Zipf–Mandelbrot law).
Zeta function regularization is used as one possible means of regularization of divergent series and divergent integrals in quantum field theory. In one notable example, the Riemann
zeta-function shows up explicitly in one method of calculating the Casimir effect. The zeta function is also useful for the analysis of dynamical systems.[34]
Infinite series
The zeta function evaluated at equidistant positive integers appears in infinite series representations of a number of constants.[35]
In fact the even and odd terms give the two sums
and
Parametrized versions of the above sums are given by
and
with 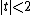 and where
and where  and
and  are the polygamma function and Euler's constant, as well as
are the polygamma function and Euler's constant, as well as
all of which are continuous at  . Other sums include
. Other sums include
where {{math|Im}} denotes the imaginary part of a complex number.
There are yet more formulas in the article Harmonic number.
==Generalizations==
There are a number of related zeta functions that can be considered to be generalizations of the Riemann zeta function. These include the Hurwitz zeta function
(the convergent series representation was given by Helmut Hasse in 1930,[36]{{inconsistent citations}} cf. Hurwitz zeta function), which coincides with the Riemann zeta function when {{math|q {{=}} 1}} (note that the lower limit of summation in the Hurwitz zeta function is 0, not 1), the Dirichlet {{mvar|L}}-functions and the Dedekind zeta-function. For other related functions see the articles zeta function and {{mvar|L}}-function.
The polylogarithm is given by
which coincides with the Riemann zeta function when {{math|z {{=}} 1}}.
The Lerch transcendent is given by
which coincides with the Riemann zeta function when {{math|z {{=}} 1}} and {{math|q {{=}} 1}} (note that the lower limit of summation in the Lerch transcendent is 0, not 1).
The Clausen function {{math|Cls(θ)}} that can be chosen as the real or imaginary part of {{math|Lis(e{{isup|iθ}})}}.
The multiple zeta functions are defined by
One can analytically continue these functions to the {{mvar|n}}-dimensional complex space. The special values taken by these functions at positive integer arguments are called multiple zeta values by number theorists and have been connected to many different branches in mathematics and physics.
Fractional derivative
In the case of the Riemann zeta function, a difficulty is represented by the fractional differentiation in the complex plane. The Ortigueira generalization of the classical Caputo fractional derivative solves this problem. The  -order fractional derivative of the Riemann zeta function is given by [37]
-order fractional derivative of the Riemann zeta function is given by [37]
Given that  is a fractional number such that
is a fractional number such that 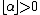 , the half-plane of convergence is
, the half-plane of convergence is 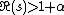 .
.
See also
- 1 + 2 + 3 + 4 + ···
- Arithmetic zeta function
- Generalized Riemann hypothesis
- Lehmer pair
- Particular values of Riemann zeta function
- Prime zeta function
- Riemann Xi function
- Renormalization
- Riemann–Siegel theta function
- ZetaGrid
Notes
2. ^This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is considered by many mathematicians to be the most important unsolved problem in pure mathematics.{{cite web|last=Bombieri|first= Enrico|url=http://www.claymath.org/sites/default/files/official_problem_description.pdf|title=The Riemann Hypothesis – official problem description|publisher=Clay Mathematics Institute|accessdate=2014-08-08|format=PDF}}
3. ^{{cite book | last = Devlin | first = Keith | authorlink = Keith Devlin | title = The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of Our Time | publisher = Barnes & Noble | year = 2002 | location = New York | pages = 43–47 | isbn = 978-0-7607-8659-8}}
4. ^{{cite book | last = Polchinski | first = Joseph | authorlink = Joseph Polchinski | title = String Theory, Volume I: An Introduction to the Bosonic String | publisher = Cambridge University Press | year = 1998 | page = 22 | isbn = 978-0-521-63303-1}}
5. ^{{cite journal|first=A. J. |last=Kainz |first2=U. M. |last2=Titulaer |title=An accurate two-stream moment method for kinetic boundary layer problems of linear kinetic equations |pages=1855–1874 |journal=J. Phys. A: Math. Gen. |volume=25 |issue=7 |date=1992|bibcode=1992JPhA...25.1855K |doi=10.1088/0305-4470/25/7/026 }}
6. ^{{cite book|authorlink=C. Stanley Ogilvy|first=C. S. |last=Ogilvy |first2=J. T. |last2=Anderson |title=Excursions in Number Theory |pages=29–35 |publisher=Dover Publications |date=1988 |isbn=0-486-25778-9}}
7. ^{{cite book|first=Charles Edward |last=Sandifer |title=How Euler Did It |publisher=Mathematical Association of America |date=2007 |page=193 |isbn=978-0-88385-563-8}}
8. ^{{cite journal|first=J. E. |last=Nymann|title=On the probability that {{mvar|k}} positive integers are relatively prime|journal=Journal of Number Theory|volume=4|year=1972|pages=469–473|doi=10.1016/0022-314X(72)90038-8|issue=5|bibcode = 1972JNT.....4..469N }}
9. ^I. V. Blagouchine The history of the functional equation of the zeta-function. Seminar on the History of Mathematics, Steklov Institute of Mathematics at St. Petersburg, 1 March 2018. [https://iblagouchine.perso.centrale-marseille.fr/Blagouchine-The-history-of-the-functional-equation-of-the-zeta-function-(1-March-2018).php PDF]
10. ^[https://link.springer.com/article/10.1007/s11139-013-9528-5 I. V. Blagouchine Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods and some related results. The Ramanujan Journal, vol. 35, no. 1, pp. 21-110, 2014. Addendum: vol. 42, pp. 777–781, 2017.] [https://iblagouchine.perso.centrale-marseille.fr/Blagouchine-Malmsten-integrals-and-their-evaluation-by-contour-integration-methods-(Ramanujan-J-2014).php PDF]
11. ^{{cite journal|first=Harold G.|last=Diamond|title=Elementary methods in the study of the distribution of prime numbers|journal=Bulletin of the American Mathematical Society|volume=7|issue=3|year=1982|pages=553–89|mr=670132|doi=10.1090/S0273-0979-1982-15057-1}}
12. ^{{cite journal | last1 = Ford | first1 = K. | year = 2002 | title = Vinogradov's integral and bounds for the Riemann zeta function | url = | journal = Proc. London Math. Soc. | volume = 85 | issue = 3| pages = 565–633 | doi = 10.1112/S0024611502013655 }}
13. ^{{cite journal|last=Voronin|first=S. M.|date=1975|title=Theorem on the Universality of the Riemann Zeta Function|journal=Izv. Akad. Nauk SSSR, Ser. Matem.|volume=39|pages=475–486}} Reprinted in Math. USSR Izv. (1975) 9: 443–445.
14. ^{{ cite journal |author1=Ramūnas Garunkštis |author2=Antanas Laurinčikas |author3=Kohji Matsumoto |author4=Jörn Steuding |author5=Rasa Steuding |title=Effective uniform approximation by the Riemann zeta-function |journal=Publicacions Matemàtiques |volume=54 |date=2010 |pages=209–219 |jstor=43736941 |doi=10.1090/S0025-5718-1975-0384673-1}}
15. ^{{ cite journal |author=Bhaskar Bagchi |title=A Joint Universality Theorem for Dirichlet L-Functions |journal=Mathematische Zeitschrift |issn=0025-5874 |volume=181 |date=1982 |pages=319–334 |doi=10.1007/bf01161980}}
16. ^{{cite book |last=Steuding |first=Jörn |date=2007 |title=Value-Distribution of L-Functions |location=Berlin |publisher=Springer |page=19 |isbn=3-540-26526-0 |series=Lecture Notes in Mathematics |doi=10.1007/978-3-540-44822-8}}
17. ^{{cite journal| first=A. A.| last=Karatsuba| title= Lower bounds for the maximum modulus of {{math|ζ(s)}} in small domains of the critical strip | pages=796–798| journal= Mat. Zametki| volume=70|issue=5| year=2001}}
18. ^{{cite journal| first=A. A.| last=Karatsuba| title= Lower bounds for the maximum modulus of the Riemann zeta function on short segments of the critical line| pages=99–104| journal= Izv. Ross. Akad. Nauk, Ser. Mat.| volume=68|issue=8| year=2004}}
19. ^{{cite journal |first=A. A. |last=Karatsuba |title=Density theorem and the behavior of the argument of the Riemann zeta function |pages=448–449 |journal=Mat. Zametki |issue=60 |year=1996}}
20. ^{{cite journal |first=A. A. |last=Karatsuba |title=On the function {{math|S(t)}}| pages=27–56| journal= Izv. Ross. Akad. Nauk, Ser. Mat. |volume=60 |issue=5 |year=1996}}
21. ^{{cite book|first=Konrad|last=Knopp|title=Theory of Functions|date=1945|pages=51–55}}
22. ^{{cite web|url=http://math.stackexchange.com/questions/117529/evaluating-the-definite-integral-int-0-infty-frac-mathrmex-left-mathr?rq=1 |title=Evaluating the definite integral...|website=math.stackexchange.com}}
23. ^{{Cite book |first=Jürgen |last=Neukirch |title=Algebraic number theory |publisher=Springer |date=1999 |page=422 |isbn=3-540-65399-6}}
24. ^{{cite web|url=http://linas.org/math/poch-zeta.pdf |format=PDF |title=A series representation for the Riemann Zeta derived from the Gauss-Kuzmin-Wirsing Operator |website=Linas.org |accessdate=2017-01-04}}
25. ^{{cite journal|first = Jonathan|last = Sondow|title = Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series|journal = Proceedings of the American Mathematical Society|year = 1994|volume = 120|issue = 2|pages = 421–424|url = http://www.ams.org/journals/proc/1994-120-02/S0002-9939-1994-1172954-7/S0002-9939-1994-1172954-7.pdf|doi = 10.1090/S0002-9939-1994-1172954-7|doi-access = free}}
26. ^{{cite journal | last = Blagouchine | first = Iaroslav V. | arxiv = 1501.00740 | doi = 10.1016/j.jnt.2015.06.012 | journal = Journal of Number Theory | pages = 365–396 | title = Expansions of generalized Euler's constants into the series of polynomials in {{pi}}−2 and into the formal enveloping series with rational coefficients only | volume = 158 | year = 2016}}
27. ^1 2 {{cite journal | last = Blagouchine | first = Iaroslav V. | arxiv = 1606.02044 | url = http://math.colgate.edu/~integers/vol18a.html | journal = Integers (Electronic Journal of Combinatorial Number Theory) | pages = 1–45 | title = Three Notes on Ser's and Hasse's Representations for the Zeta-functions | volume = 18A | year = 2018| bibcode = 2016arXiv160602044B}}
28. ^{{cite journal|first = Joseph|last = Ser|authorlink = Joseph Ser|title = Sur une expression de la fonction ζ(s) de Riemann|trans-title = Upon an expression for Riemann's ζ function|year = 1926|journal = Comptes rendus hebdomadaires des séances de l'Académie des Sciences|volume = 182|pages = 1075–1077|language = French}}
29. ^{{cite journal|title = A New Proof of H. Hasse's Global Expression for the Riemann's Zeta Function|year = 2017|first = Demetrios P.|last = Kanoussis|url = https://www.researchgate.net/publication/317823796_A_New_Proof_of_HHasse%27s_Global_Expression_for_the_Riemann%27s_Zeta_Function}}
30. ^{{cite book|first = Peter|last = Borwein|authorlink = Peter Borwein|url = http://www.cecm.sfu.ca/personal/pborwein/PAPERS/P155.pdf|chapter = An Efficient Algorithm for the Riemann Zeta Function|series = Conference Proceedings, Canadian Mathematical Society|year = 2000|title = Constructive, Experimental, and Nonlinear Analysis|volume = 27|pages = 29–34|isbn = 978-0-8218-2167-1|editor-first = Michel A.|editor-last = Théra|publisher = American Mathematical Society, on behalf of the Canadian Mathematical Society|location = Providence, RI}}
31. ^{{cite journal|first=István|last=Mező|title=The primorial and the Riemann zeta function|journal= The American Mathematical Monthly|year=2013|volume=120|issue=4|page=321}}
32. ^{{cite journal|first1=Takao|last1=Komatsu|first2=István|last2=Mező|title=Incomplete poly-Bernoulli numbers associated with incomplete Stirling numbers|journal=Publicationes Mathematicae Debrecen|year=2016|volume=88|issue=3–4|pages=357–368|doi=10.5486/pmd.2016.7361|url=https://arxiv.org/pdf/1510.05799|arxiv=1510.05799}}
33. ^1 {{cite arxiv|last=Fischer|first=Kurt|date=2017-03-04|title=The Zetafast algorithm for computing zeta functions|eprint=1703.01414}}
34. ^{{cite web|url=http://empslocal.ex.ac.uk/people/staff/mrwatkin/zeta/spinchains.htm |title=Work on spin-chains by A. Knauf, et. al |website=Empslocal.ex.ac.uk |date= |accessdate=2017-01-04}}
35. ^Most of the formulas in this section are from § 4 of J. M. Borwein et al. (2000)
36. ^1 2 {{Cite journal |first=Helmut |last=Hasse |authorlink=Helmut Hasse |title=Ein Summierungsverfahren für die Riemannsche {{mvar|ζ}}-Reihe |trans-title=A summation method for the Riemann ζ series |year=1930 |journal=Mathematische Zeitschrift |volume=32 |issue=1 |pages=458–464 |doi=10.1007/BF01194645 |language=German}}
37. ^{{cite book | last1 = Guariglia | first1 = E. | year = 2015 | title=Fractional derivative of the Riemann zeta function | publisher= In: Fractional Dynamics (Cattani, C., Srivastava, H., and Yang, X. Y.). De Gruyter|pages=357–368 | doi = 10.1515/9783110472097-022 }}
References
- {{dlmf|id=25|first=T. M. |last=Apostol|title=Zeta and Related Functions}}
- {{cite journal|author1-link=Jonathan Borwein|first1=Jonathan|last1=Borwein |first2=David M. |last2=Bradley |author3-link=Richard Crandall|first3=Richard|last3=Crandall
| url = http://www.maths.ex.ac.uk/~mwatkins/zeta/borwein1.pdf|format=PDF
| title = Computational Strategies for the Riemann Zeta Function| journal=J. Comp. App. Math.| year=2000| volume=121
| pages=247–296
|doi=10.1016/S0377-0427(00)00336-8
|issue=1–2|bibcode = 2000JCoAM.121..247B }}
- {{cite journal
|first1=Djurdje
|last1= Cvijović
|first2=Jacek
|last2= Klinowski
| title = Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments
| journal=J. Comp. App. Math.| year=2002| volume=142| pages=435–439
| doi = 10.1016/S0377-0427(02)00358-8
|mr=1906742
|issue=2|bibcode=2002JCoAM.142..435C}}
- {{cite journal
| first1=Djurdje
|last1= Cvijović
|first2= Jacek
|last2= Klinowski
| title = Continued-fraction expansions for the Riemann zeta function and polylogarithms| journal=Proc. Amer. Math. Soc.| year=1997| volume=125| pages=2543–2550| doi = 10.1090/S0002-9939-97-04102-6
| issue=9}}
- {{cite book|first=H. M. |last=Edwards|authorlink=Harold Edwards (mathematician)| title=Riemann's Zeta Function|publisher=Academic Press|year=1974|isbn=0-486-41740-9}} Has an English translation of Riemann's paper.
- {{cite journal | last1 = Hadamard | first1 = Jacques | authorlink = Jacques Hadamard | year = 1896 | title = Sur la distribution des zéros de la fonction {{math|ζ(s)}} et ses conséquences arithmétiques | url = | journal = Bulletin de la Société Mathématique de France | volume = 14 | issue = | pages = 199–220 }}
- {{cite book|authorlink=G. H. Hardy|first=G. H.|last=Hardy|title=Divergent Series|publisher=Clarendon Press, Oxford|year=1949}}
- {{cite journal
|authorlink=Helmut Hasse
|first1=Helmut
|last1=Hasse
|title=Ein Summierungsverfahren für die Riemannsche {{mvar|ζ}}-Reihe
|year=1930
|journal=Math. Z.
|volume=32
|pages=458–464
|mr=1545177
|doi=10.1007/BF01194645
}} (Globally convergent series expression.)
- {{cite book|first=A. |last=Ivic|title=The Riemann Zeta Function|publisher=John Wiley & Sons|year=1985|isbn=0-471-80634-X}}
- {{cite book | first=Y. |last=Motohashi | title=Spectral Theory of the Riemann Zeta-Function | publisher= Cambridge University Press | year=1997| isbn=0521445205}}
- {{cite book|author1-link=A. A. Karatsuba|first1=A. A.|last1= Karatsuba |first2= S. M.|last2= Voronin|title=The Riemann Zeta-Function|publisher= W. de Gruyter|location= Berlin|year=1992}}
- {{cite journal
|first1=István
|last1=Mező
|first2=Ayhan
|last2=Dil
|doi=10.1016/j.jnt.2009.08.005
|title=Hyperharmonic series involving Hurwitz zeta function
|journal= Journal of Number Theory
|year=2010
|volume=130
|issue=2
|pages=360–369
|mr=2564902
}}
- {{cite book| first=Hugh L.|last= Montgomery| authorlink=Hugh Montgomery (mathematician)|first2=Robert C. |last2=Vaughan |authorlink2=Robert Charles Vaughan (mathematician) | title=Multiplicative number theory. I. Classical theory| series=Cambridge tracts in advanced mathematics| volume=97| publisher=Cambridge University Press| year=2007| isbn=0-521-84903-9|at=Ch. 10}}
- {{cite book| authorlink=Donald J. Newman| first1=Donald J. |last1=Newman| title=Analytic number theory| series=Graduate Texts in Mathematics| volume=177| publisher=Springer-Verlag| year=1998| isbn=0-387-98308-2 |at=Ch. 6}}
- {{cite journal
|first1=Guo
|last1=Raoh
|title=The Distribution of the Logarithmic Derivative of the Riemann Zeta Function
|journal=Proceedings of the London Mathematical Society
|year=1996
|volume=s3–72
|doi=10.1112/plms/s3-72.1.1
|pages=1–27
|arxiv=1308.3597
}}
- {{Cite journal|first=Bernhard|last=Riemann|url=http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Zeta/|title=Über die Anzahl der Primzahlen unter einer gegebenen Grösse|year=1859|journal=Monatsberichte der Berliner Akademie}}. In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953).
- {{cite journal
|first1=Jonathan
|last1=Sondow
|doi=10.1090/S0002-9939-1994-1172954-7
|title= Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series
|journal=Proc. Amer. Math. Soc.
|year=1994
|pages=421–424
|issue=2
|volume=120
|url=http://www.ams.org/journals/proc/1994-120-02/S0002-9939-1994-1172954-7/S0002-9939-1994-1172954-7.pdf
}}
- {{cite book|authorlink=Edward Charles Titchmarsh|first=E. C.|last=Titchmarsh|title=The Theory of the Riemann Zeta Function, |edition=2nd rev. |editor=Heath-Brown|publisher=Oxford University Press|year= 1986}}
- {{cite book|author1-link=E. T. Whittaker|first1=E. T.|last1=Whittaker|author2-link=G. N. Watson|first2=G. N.|last2=Watson|date=1927|title=A Course in Modern Analysis|edition=4th|publisher=Cambridge University Press|at=Ch. 13}}
- {{cite journal|first1=Jianqiang
|last1=Zhao
|doi=10.1090/S0002-9939-99-05398-8
| title = Analytic continuation of multiple zeta functions| journal=Proc. Amer. Math. Soc.| year=1999| volume=128| pages=1275–1283|mr=1670846|issue=5
}}
External links
- {{springer|title=Zeta-function|id=p/z099260}}
- Riemann Zeta Function, in Wolfram Mathworld — an explanation with a more mathematical approach
- Tables of selected zeros
- Prime Numbers Get Hitched A general, non-technical description of the significance of the zeta function in relation to prime numbers.
- [https://arxiv.org/abs/math/0309433v1 X-Ray of the Zeta Function] Visually oriented investigation of where zeta is real or purely imaginary.
- Formulas and identities for the Riemann Zeta function functions.wolfram.com
- Riemann Zeta Function and Other Sums of Reciprocal Powers, section 23.2 of Abramowitz and Stegun
- {{cite web|last=Frenkel|first=Edward|author-link=Edward Frenkel|title=Million Dollar Math Problem|url=https://www.youtube.com/watch?v=d6c6uIyieoo|publisher=Brady Haran|accessdate=11 March 2014|format=video}}
- Mellin transform and the functional equation of the Riemann Zeta function—Computational examples of Mellin transform methods involving the Riemann Zeta Function
- Elisenda de Sant Climent
- Elisenda Fabregas
- Elisenda Grigsby
- Elisenda Vives Balmaña
- Elise Neumann Hedinger
- Elisenhøy
- Eliseo Branca
- Eliseo Calenzio
- Eliseo Canaveri
- Elise O'Dea
- Eliseo Falcón Falcón
- Eliseo Morales
- Eliseo Nicolás Alonso
- Eliseo Rio
- Eliseo Rio, Jr.
- Eliseo Rio Jr.
- Eliseo Roberto Colon Zayas
- Eliseo Rodriguez
- Eliseo Theatre
- Elise Otte
- Elise Ottsen-Jensen
- Eliseo Vidal
- Eliseo Vivas
- Elise Perry
- Elise Pfister