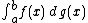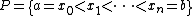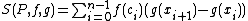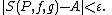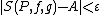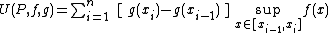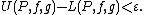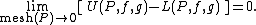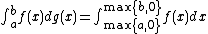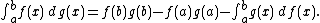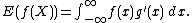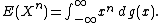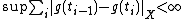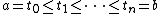“Riemann–Stieltjes integral”的意思、由来-开放百科全书

词条

Riemann–Stieltjes integral

释义

Definition
Generalized Riemann–Stieltjes integral Darboux sums
Examples
Riemann Integral Differentiable RELU
Properties
Existence of the integral
Application to functional analysis
Generalization
Notes
References

In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition of this integral was first published in 1894 by Stieltjes.^[1] It serves as an instructive and useful precursor of the Lebesgue integral, and an invaluable tool in unifying equivalent forms of statistical theorems that apply to discrete and continuous probability.

Definition

The Riemann–Stieltjes integral of a real-valued function of a real variable with respect to a real function is denoted by

and defined to be the limit, as the norm (or mesh) of the partition (i.e. the length of the longest subinterval)

of the interval [a, b] approaches zero, of the approximating sum

where is in the i-th subinterval [x_i, x_i+1]. The two functions and are respectively called the integrand and the integrator. Typically is taken to be monotone (or at least of bounded variation) and right-semicontinuous (however this last is essentially convention). We specifically do not require to be continuous, which allows for integrals that have point mass terms.

The "limit" is here understood to be a number A (the value of the Riemann–Stieltjes integral) such that for every ε > 0, there exists δ > 0 such that for every partition P with mesh(P) < δ, and for every choice of points c_i in [x_i, x_i+1],

Generalized Riemann–Stieltjes integral

A slight generalization, introduced by {{harvtxt|Pollard|1920}} and now standard in analysis, is to consider in the above definition partitions P that refine another partition P_ε, meaning that P arises from P_ε by the addition of points, rather than from partitions with a finer mesh. Specifically, the generalized Riemann–Stieltjes integral of f with respect to g is a number A such that for every ε > 0 there exists a partition P_ε such that for every partition P that refines P_ε,

for every choice of points c_i in [x_i, x_i+1].

This generalization exhibits the Riemann–Stieltjes integral as the Moore–Smith limit on the directed set of partitions of [a, b] {{harv|McShane|1952}}. {{harvtxt|Hildebrandt|1938}} calls it the Pollard–Moore–Stieltjes integral.

Darboux sums

The Riemann–Stieltjes integral can be efficiently handled using an appropriate generalization of Darboux sums. For a partition P and a nondecreasing function g on [a, b] define the upper Darboux sum of f with respect to g by

and the lower sum by

.

Then the generalized Riemann–Stieltjes of f with respect to g exists if and only if, for every ε > 0, there exists a partition P such that

Furthermore, f is Riemann–Stieltjes integrable with respect to g (in the classical sense) if

See {{harvtxt|Graves|1946|loc=Chap. XII, §3}}.

Examples

Riemann Integral

Of course, the standard Riemann integral is an example of the Riemann-Stieltjes integral if is taken as .

Differentiable

Given a which is continuously differentiable over it can be shown that there is the equality

where the integral on the right-hand side is the standard Riemann-integral. This of course assumes that is already integrable for this Riemann-Stieltjes integral. More generally, the Riemann integral equals the Riemann–Stieltjes integrals if is the (Lebesgue) integral of its derivative; in this case is said to be absolutely continuous. It may be the case that has jump discontinuities, or may have derivative zero almost everywhere while still being continuous and increasing (for example, could be the Cantor function or Devil's staircase), in either of which cases the Riemann–Stieltjes integral is not captured by any expression involving derivatives of g.

RELU

Consider the function 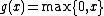called the RELU. Then the Riemann-Stieltjes can be evaluated as

where the integral on the right-hand side is the standard Riemann integral.

Properties

The Riemann–Stieltjes integral admits integration by parts in the form

and the existence of either integral implies the existence of the other {{harv|Hille|Phillips|1974|loc=§3.3}}.

Existence of the integral

The best simple existence theorem states that if f is continuous and g is of bounded variation on [a, b], then the integral exists.^[2] A function g is of bounded variation if and only if it is the difference between two (bounded) monotone functions. If g is not of bounded variation, then there will be continuous functions which cannot be integrated with respect to g. In general, the integral is not well-defined if f and g share any points of discontinuity, but there are other cases as well.

On the other hand, a classical result of {{harvtxt|Young|1936}} states that the integral is well-defined if f is α-Hölder continuous and g is β-Hölder continuous with α + β > 1.

==Application to probability theory==

If g is the cumulative probability distribution function of a random variable X that has a probability density function with respect to Lebesgue measure, and f is any function for which the expected value E(|f(X)|) is finite, then the probability density function of X is the derivative of g and we have

But this formula does not work if X does not have a probability density function with respect to Lebesgue measure. In particular, it does not work if the distribution of X is discrete (i.e., all of the probability is accounted for by point-masses), and even if the cumulative distribution function g is

continuous, it does not work if g fails to be absolutely continuous (again, the Cantor function may serve as an example of this failure). But the identity

holds if g is any cumulative probability distribution function on the real line, no matter how ill-behaved. In particular, no matter how ill-behaved the cumulative distribution function g of a random variable X, if the moment E(Xⁿ) exists, then it is equal to

Application to functional analysis

The Riemann–Stieltjes integral appears in the original formulation of F. Riesz's theorem which represents the dual space of the Banach space C[a,b] of continuous functions in an interval [a,b] as Riemann–Stieltjes integrals against functions of bounded variation. Later, that theorem was reformulated in terms of measures.

The Riemann–Stieltjes integral also appears in the formulation of the spectral theorem for (non-compact) self-adjoint (or more generally, normal) operators in a Hilbert space. In this theorem, the integral is considered with respect to a spectral family of projections. See {{harvtxt|Riesz|Sz. Nagy|1955}} for details.

Generalization

An important generalization is the Lebesgue–Stieltjes integral which generalizes the Riemann–Stieltjes integral in a way analogous to how the Lebesgue integral generalizes the Riemann integral. If improper Riemann–Stieltjes integrals are allowed, the Lebesgue integral is not strictly more general than the Riemann–Stieltjes integral.

The Riemann–Stieltjes integral also generalizes {{Citation needed|date=March 2019}} to the case when either the integrand ƒ or the integrator g take values in a Banach space. If {{nowrap|g : [a,b] → X}} takes values in the Banach space X, then it is natural to assume that it is of strongly bounded variation, meaning that

the supremum being taken over all finite partitions

of the interval [a,b]. This generalization plays a role in the study of semigroups, via the Laplace–Stieltjes transform.

Notes

1. ^{{harvnb|Stieltjes|1894|pp=68–71}}.
2. ^{{harvnb|Johnsonbaugh|Pfaffenberger|2010}}, page 219. {{harvnb|Rudin|1964}}, pages 121–122. {{harvnb|Kolmogorov|Fomin|1970}}, page 368.

References

{{citation | last=Graves|first=Lawrence|title=The theory of functions of a real variable|publisher=McGraw–Hill|year=1946}}.
{{Citation | last1=Hildebrandt | first1=T. H. | title=Definitions of Stieltjes Integrals of the Riemann Type | mr=1524276 | year=1938 | journal=The American Mathematical Monthly | issn=0002-9890 | volume=45 | issue=5 | pages=265–278|jstor=2302540}}.
{{Citation | last1=Hille | first1=Einar | authorlink1=Einar Hille | last2=Phillips | first2=Ralph S. | authorlink2=Ralph Phillips (mathematician) | title=Functional analysis and semi-groups | publisher=American Mathematical Society | location=Providence, R.I. | mr=0423094 | year=1974}}.
{{citation| title = Foundations of mathematical analysis| last1 = Johnsonbaugh| first1 = Richard F.| last2= Pfaffenberger|first2= William Elmer| year = 2010| publisher = Dover Publications|location=Mineola, New York| isbn= 978-0-486-47766-4}}.
{{citation| title = Introductory Real Analysis| last1 = Kolmogorov| first1 = Andrey| authorlink1 = Andrey Kolmogorov| last2= Fomin|first2= Sergei V.| authorlink2 = Sergei Fomin| year = 1970| edition = Revised English edition, trans. by Richard A. Silverman (1975)| publisher = Dover Press| isbn= 0-486-61226-0}}.
{{citation|first=E. J.|last=McShane|url=https://www.maa.org/sites/default/files/pdf/upload_library/22/Chauvenet/Mcshane.pdf|title=Partial orderings & Moore-Smith limit|accessdate=2 November 2010|journal=The American Mathematical Monthly|volume=59|year=1952|pages=1–11|doi=10.2307/2307181|jstor=2307181}}.
{{citation|first=Henry|last=Pollard|title=The Stieltjes integral and its generalizations|year=1920|volume=19|journal=The Quarterly Journal of Pure and Applied Mathematics}}.
{{citation|first1=F.|last1=Riesz|first2=B.|last2=Sz. Nagy|title=Functional Analysis|year=1990|publisher=Dover Publications|isbn=0-486-66289-6}}.
{{citation| title = Principles of mathematical analysis| last1 = Rudin| first1 = Walter|edition = Second| year = 1964| publisher = McGraw-Hill|location=New York}}.
{{citation|last1=Shilov|first1=G. E.|last2=Gurevich|first2=B. L.|year=1978|title=Integral, Measure, and Derivative: A Unified Approach|journal=Integral|publisher=Dover Publications|isbn=0-486-63519-8|bibcode=1966imdu.book.....S}}, Richard A. Silverman, trans.
{{Citation | last1=Stieltjes | first1=Thomas Jan|authorlink1=Thomas Joannes Stieltjes|title=Recherches sur les fractions continues | url=http://www.numdam.org/numdam-bin/item?id=AFST_1894_1_8_4_J1_0 | mr = 1344720 | year=1894 | journal=Ann. Fac. Sci. Toulouse | volume=VIII | pages=1–122}}
{{citation|last=Stroock|first=Daniel W.|year=1998|title=A Concise Introduction to the Theory of Integration|publisher=Birkhauser|edition=3rd|isbn=0-8176-4073-8}}.
{{citation | last=Young|first=L.C.|title=An inequality of the Hölder type, connected with Stieltjes integration|journal=Acta Mathematica|volume=67|year=1936|issue=1|pages=251–282|doi=10.1007/bf02401743}}.

2 : Definitions of mathematical integration|Bernhard Riemann

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。