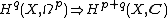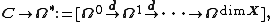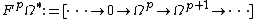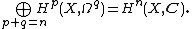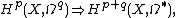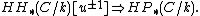1. Description of the spectral sequence

2. Degeneration

3. Purely algebraic proof

4. Non-commutative version

5. See also

6. References

In mathematics, the Hodge–de Rham spectral sequence (named after W. V. D. Hodge and Georges de Rham), also known as the Frölicher spectral sequence (after Alfred Frölicher) computes the cohomology of a complex manifold.

Description of the spectral sequence

The spectral sequence is as follows:

where X is a complex manifold, 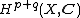is its cohomology with complex coefficients and the left hand term, which is the -page of the spectral sequence, is the cohomology with values in the sheaf of holomorphic differential forms.

The existence of the spectral sequence as stated above follows from the Poincaré lemma, which gives a quasi-isomorphism of complexes of sheaves

together with the usual spectral sequence resulting from a filtered object, in this case the Hodge filtration

of .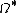

Degeneration

The central theorem related to this spectral sequence is that for a compact Kähler manifold X, for example a projective variety, the above spectral sequence degenerates at the -page. In particular, it gives an isomorphism referred to as the Hodge decomposition

The degeneration of the spectral sequence can be shown using Hodge theory.^[1][2] An extension of this degeneration in a relative situation, for a proper smooth map , was also shown by Deligne.^[3]

Purely algebraic proof

For smooth proper varieties over a field of characteristic 0, the spectral sequence can also be written as

where 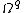denotes the sheaf of algebraic differential forms (also known as Kähler differentials) on X, 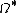is the (algebraic) de Rham complex, consisting of the 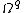with the differential being the exterior derivative. In this guise, all terms in the spectral sequence are of purely algebraic (as opposed to analytic) nature. In particular, the question of the degeneration of this spectral sequence makes sense for varieties over a field of characteristic p>0.

Non-commutative version

The de Rham complex and also the de Rham cohomology of a variety admit generalizations to non-commutative geometry. This more general setup studies dg categories. To a dg category, one can associate its Hochschild homology, and also its periodic cyclic homology. When applied to the category of perfect complexes on a smooth proper variety X, these invariants give back differential forms, respectively, de Rham cohomology of X. Kontsevich and Soibelman conjectured in 2009 that for any smooth and proper dg category C over a field of characteristic 0, the Hodge-de Rham spectral sequence starting with Hochschild homology and abutting to periodic cyclic homology, degenerates:

This conjecture was proved by {{harvtxt|Kaledin|2008}} and {{harvtxt|Kaledin|2016}} by adapting the above idea of Deligne and Illusie to the generality of smooth and proper dg-categories. {{harvtxt|Mathew|2017}} has given a proof of this degeneration using topological Hochschild homology.

See also

• Frölicher spectral sequence
• Hodge theory

References

• {{citation|author1-link=Pierre Deligne|author2-link=Luc Illusie|author1=Deligne|first1=Pierre|author2=Illusie|first2=Luc|title=Relèvements modulo p² et décomposition du complexe de de Rham|journal=Invent. Math.|volume=89|issue=89|pages=247–270|year=1987|doi=10.1007/bf01389078|bibcode=1987InMat..89..247D}}

• {{citation|author1=Kaledin|first1=D.|title=Non-commutative Hodge-to-de Rham degeneration via the method of Deligne-Illusie|journal=Pure and Applied Mathematics Quarterly|volume=4|year=2008|issue=3|pages=785–876|mr=2435845|doi=10.4310/PAMQ.2008.v4.n3.a8|arxiv=math/0611623}}

• {{citation|author1=Kaledin|first1=Dmitry|title=Spectral sequences for cyclic homology|arxiv=1601.00637|year=2016|bibcode=2016arXiv160100637K}}

• {{citation|author1=Mathew|first1=Akhil|title=Kaledin's degeneration theorem and topological Hochschild homology|year=2017|arxiv=1710.09045|bibcode=2017arXiv171009045M}}

• Monument of Graf Vorontsov, Odessa
• Monument of Gratitude to France
• Monument of Humanity
• Monument of Lysicrates
• Monument of Piazza Mentana
• Monument of Prusias II
• Monument of Prusias II (Delphi)
• Monument of Sari Ashig
• Monument of States
• Monument of the End
• Monument of the Four Moors
• Monument of the Great October Revolution (Rostov-on-Don)
• Monument of the War of Independence
• Monument of Virgin Mary Monument, Timișoara
• Monumento LRT station
• Monumento LRT Station
• Monumento Natural das Árvores Fossilizadas
• Monument One
• Monumento Rodoviário da Rodovia Presidente Dutra
• Monumento às Bandeiras
• Monument Peak (Nevada)
• Monument Peak (San Bernardino County)
• Monument Peak (San Bernardino Mountains)
• Monument Point
• Monument Point (Arrow episode)