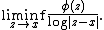“Lelong number”的意思、由来-开放百科全书

词条

Lelong number

释义

Definitions
References

In mathematics, the Lelong number is an invariant of a point of a complex analytic variety that in some sense measures the local density at that point. It was introduced by {{harvs|txt|last=Lelong|authorlink=Pierre Lelong|year=1957}}. More generally a closed positive (p,p) current u on a complex manifold has a Lelong number n(u,x) for each point x of the manifold. Similarly a plurisubharmonic function also has a Lelong number at a point.

Definitions

The Lelong number of a plurisubharmonic function φ at a point x of Cⁿ is

For a point x of an analytic subset A of pure dimension k, the Lelong number ν(A,x) is the limit of the ratio of the areas of A ∩ B(r,x) and a ball of radius r in C^k as the radius tends to zero. (Here B(r,x) is a ball of radius r centered at x.) In other words the Lelong number is a sort of measure of the local density of A near x. If x is not in the subvariety A the Lelong number is 0, and if x is a regular point the Lelong number is 1. It can be proved that the Lelong number ν(A,x) is always an integer.

References

{{Citation | last1=Lelong | first1=Pierre | title=Intégration sur un ensemble analytique complexe | url=http://www.numdam.org/item?id=BSMF_1957__85__239_0 |mr=0095967 | year=1957 | journal=Bulletin de la Société Mathématique de France | issn=0037-9484 | volume=85 | pages=239–262}}
{{Citation | last1=Lelong | first1=Pierre | title=Fonctions plurisousharmoniques et formes différentielles positives | url=https://books.google.com/books/about/Fonctions_plurisousharmoniques_et_formes.html?id=cy_vAAAAMAAJ | publisher=Gordon & Breach | location=Paris |mr=0243112 | year=1968}}
{{Citation | last1=Varolin | first1=Dror | editor1-last=McNeal | editor1-first=Jeffery | editor2-last=Mustaţă | editor2-first=Mircea | title=Analytic and algebraic geometry | publisher=American Mathematical Society | location=Providence, R.I. | series=IAS/Park City Math. Ser. | isbn= 978-0-8218-4908-8 |mr=2743817 | year=2010 | volume=17 | chapter=Three variations on a theme in complex analytic geometry | chapterurl=https://books.google.com/books?id=wwgEP4frWvAC&pg=PA183 | pages=183–294}}

1 : Complex manifolds

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。