回归分析huigui fenxi
“回归”原是生物学的词汇。英国科学家F·高尔顿在研究中发现：父母的身高与其子女的身高有一定的关系，即子女的身高向其父母的平均身高方向趋近，这种趋近现象称为“回归”。后来以此名词泛指变量间的这种关系。变量之间的关系一般可分为两类。一类是一种完全确定的关系，即称函数关系，如圆面积A与半径R的函数关系为A=πR2。另一类是一种不完全确定的关系，即称相关关系，如身高与体重的关系中，一般说来身高者体也重，但也有身高者体并不重的。在教育上较多的是相关关系。回归分析就是处理多个变量间相关关系的一种数学方法，它主要解决：❶确定几个特定变量之间是否存在相关关系？如是，则要找出它们之间的合适数学表达式；
❷根据一个或几个变量的值，预测或控制另一个变量的取值，并要知道这种预测的精确度；
❸进行因素分析，找出主要变量和次要变量等。
回归与相关有联系也有区别。相关表示两个变量之间的双方向的关系，而回归表示一个变量随另一个变量变化的单方向的关系。
回归分析的主要内容有一元线性回归、二元线性回归和多元线性回归等。其中的“元”是指自变量的个数。这里着重介绍一元线性回归。
一元线性回归直线的计算 假定变量X与Y之间存在某种相关关系，而我们想以变量X来估计Y；这时X为自变量，Y为因变量。通过实验或观测，我们可以找到关于X与Y的若干数据；然后通过这些数据找到一条能描述这两个变量间关系的数学表达式（亦称经验公式）。若它们的关系是呈一直线，则称为一元线性回归直线。其一般形式为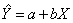
式中 Y——X的估计值
a和b——回归方程的常数项和回归系数。其中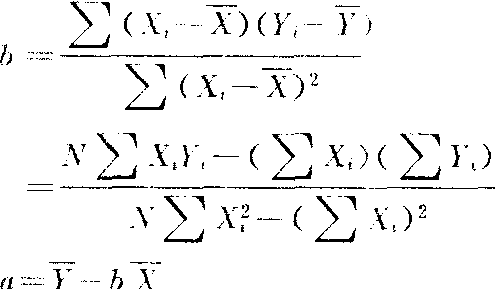
式中 N——数据(X1,Y1)的对数
[例1] 某中学12个学生的初二和初三的数学统考成绩如下。求其回归方程。
| 初二 | 63 | 53 | 52 | 58 | 88 | 60 | 62 | 56 | 76 | 55 | 90 | 49 |
| 初三 | 60 | 50 | 71 | 57 | 98 | 67 | 87 | 47 | 87 | 71 | 96 | 51 |
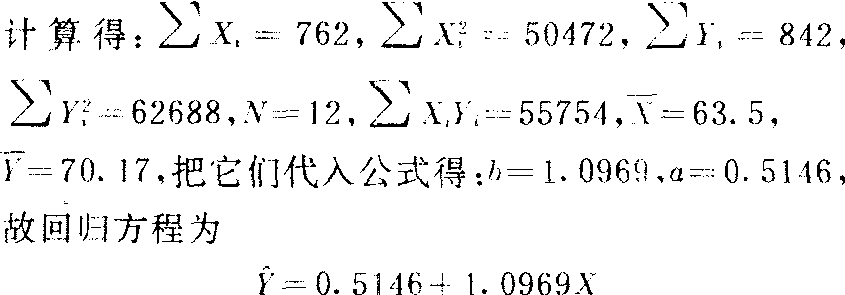
回归方程的效果 这个问题具体指：❶回归系数b是否显著？若显著，则回归或预测效果较好。
❷回归效率有多大？即能被预测的成分占总成分的比例有多少。为此必须先对回归方程进行统计检验。检验的方法是对回归方程进行方差分析，即把因变量(Y)之间的总变差(SST)分解成自变量(X)之间的变差(SSU)和剩余变差(SSQ):
SST=SSL+SSQ
式中 SSU——回归平方和，属一种预测的变差
SSQ——剩余平方和，属一种非预测的变差
它们的方差分析表如下：
a=0.01及f1 =1和f2＝ 10查F分布表得F(1.10)0.01＝10.0。由F>F(1,10)0.01＝10，故拒绝假设H0，即回归方程的回归系数有极显著的意义，亦即回归方程的效果很好。
回归方程的效率是回归变差在总变差中所占的比重，即
式中 r——相关系数
其余符号同前。
从式中亦可知，回归效率恰为相关系数的平方。
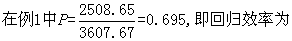69.5%。注意：如果F检验不显著，则有下列几种可能：❶影响Y的因素除X外，至少还有一个不可忽视的因素；
❷X和Y是非线性关系；
❸X与Y无关。
利用回归方程进行预测 从统计观点来看，所谓预测就是一个区间估计问题。即在回归方程中，在一定的置信水平α下，找出一个正数δ，使得某自变量X0所对应的实际观测值Ŷ0以(1-α)的概率落在(Ŷ0-δ,Ŷ+δ)之内，即
或
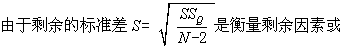
称随机因素波动程度的指标。显然，S愈小即随机因素的波动愈小，则对Y0的预测就愈准确(即估计值Y0愈接近于Y0)。因此S是回归方程中预测Y0的精确度的指标。设X0来自于正态分布，则它所对应的Y0和Y0也服从于正态分布，因而Y0-Ŷ0也服从于正态分布。这就是说，当X=X0时，实际观测值Y0是以估计值Ŷ0为中心而正态地分布着，并且它与S之间有下述关系：
Y0落在Ŷ0±S内的概率约为0.683(68.3%);
Y0落在Ŷ0±2S内的概率约为0.954(95.4%);
Y0落在Ŷ0±3S内的概率约为0.997(99.7%)。
就一般而言，Y0落在下面二直线之间的概率为1-a:
故Y0落在这2条直线内的概率为95%以上。
多元线性回归的方法与一元线性回归的思想基本相同，其回归方程为
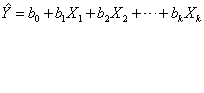
任何两个变量之离差积的平方和为
则关于b1,b2，…，bk的正规方程组为
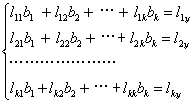
解这一正规方程组可得：b1,b2，…，bk;
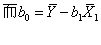
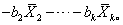
多元线性回归的方差分析表如下：
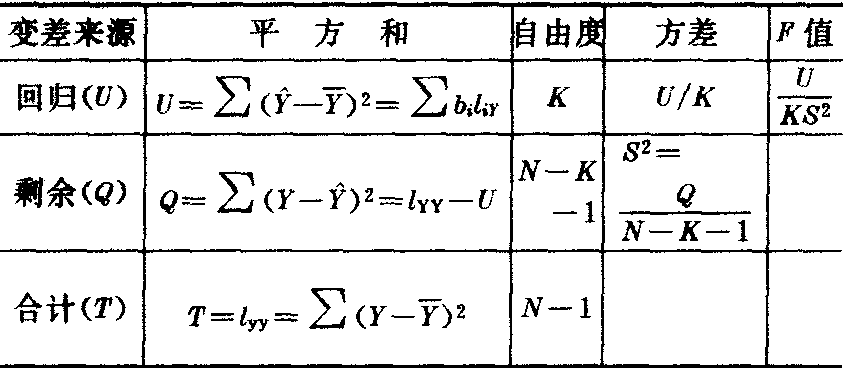
检验多元线性回归的效果是用复相关系数：
K2为回归效率。R与相关系数r的意义相同，但0≤R≤1；其检验方法亦与r相同，但自由度为N-K。
回归分析huigui fenxi
根据变量间的数量关系的模型来预测其中一些变量的状态的方法。由于描述、预测和控制是心理学研究的主要目的，因此，作为预测方法之一的回归分析具有很重要的意义。一般来说，回归系数越高，预测越精确；反之，预测的误差越大。回归分析主要有：
❶一元线性回归。变量之间关系的数学表达式是一次函数，一次函数在坐标图上以直线表示，对这种关系的回归分析就是线性回归分析。只有一个自变量的线性回归叫一元线性回归。如根据学生智力测验的智商分数预测其学习成绩。
❷多元线性回归。自变量是两个或两个以上时的线性回归分析。其基本假定、原理及基本计算过程与一元线性回归是相同的。
❸曲线回归。有些变量之间关系的数学模型是曲线方程，由于按方程作出的曲线并没有一定的规律、趋势，因此，曲线回归一般用于描述而不用于预测，在心理学的实际研究中应用很少。
回归分析
数理统计的一个内容。详“相关分析”。