堆算Duisuan
古代埃及人把未知数称为“堆”,本意似乎是指数量未知的谷物的堆。阿默斯纸草书(参见该条)中有一类关于“堆算”的问题,其中一个是:“有一堆,它的2/3、它的1/2、它的1/7,再加上它的全部,共为37”, 下图给出了这一问题的埃及象形文字写法和经简化的僧侣文字写法: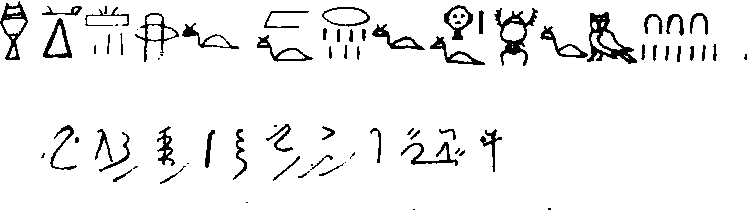
为了求出这一“堆”的数量,书中使用了假设法(又称试位法)求解, 用今天的记法相当于: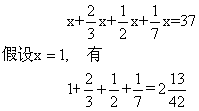
但正确结果应是37, 因此取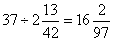
这就是所求的答案。
阿默斯纸草书的第63题是: “把700块面包分发
数的系数, 那么这个问题就相当于
上面两个问题在今天看来都属于一元一次方程问题。但是,如果据此就认为古代埃及人已经有了一元一次方程的明确概念,理由就不十分充足了。实际上,在中国 《九章算术》中有一类“衰分”问题(参见“比例分配”),可概括为:把总数是A的一批物品按照比率a1:a2:a3: ……:an分为n份,用今天的数学符号表示就是:
已知 x1+x2+……+xn =A
x1:x2: ……: xn=a1: a2: ……: an
求 x1, x2, x3, ……, xn
这与阿默斯纸草书第63题是十分相似的。《九章算术》是用比例算法求解的。
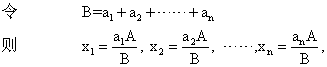
这实质上就是阿默斯纸草书中的方法。因此,实际的情况应该是:埃及人熟练地运用比例算法,解决了今天可归入一元一次方程的一些问题。
由阿默斯纸草书第63题, 还使我们联想到中国《孙子算经》 (参见“算经十书”) 中著名的 “河上荡杯”题:“今有妇人河上荡杯(注:荡杯,即洗碗)。津吏问曰: ‘杯何以多?’ 妇人曰: ‘家有客。’ 津吏曰:“客几何?’妇人曰: ‘二人共饭(注:二人共用一只碗吃饭),三人共羹, 四人共肉,凡用杯六十五,不知客几何。’”解法是:“置六十五杯,以一十二乘之,得七百八十,以一十三除之,即得。”由这一过程可明确看出,《孙子算经》的作者是用求解一元一次方程的方法解这道题的。用今天的记法, 设人数为x, 由已知: