对策论game theory

研究对策现象的数学理论和方法，也称博奕论。对策是决策者在竞争状态下进行的决策，是参加竞争的各方为了自己获胜而采取的对付对方的策略。1944年冯·诺伊曼(J.vonNeumann)和摩根斯特恩(O.Morgenstern)合著的《对策论与经济行为》对对策论进行了系统的研究。开始应用到经济方面，并逐步扩展到军事、政治学、心理学等领域。
任何一个对策活动都包括三个基本要素： 局中人、策略和得失函数。参与竞争活动的各方称为局中人。局中人可以是个人或组织。策略指局中人据以选择其行动方案的规则，全部策略称为策略集。假定局中人都是明智的，并且都知道对方的策略集。如策略个数有限，为有限对策，否则为无限对策。得失函数是用数量表示的对策结局。从每个局中人的策略集中各取一个策略组成的一个策略组，称为局势。对策分为静态对策和动态对策。静态对策可按局中人的数量、有无结盟、策略数是否有限以及得失之和是否为零来分类。动态对策有多阶段对策、微分对策等。
二人有限零和对策 设局中人为甲、乙双方，分别有m和n个策略，在任一局势中全体局中人的得失相加总是等于零。其得失可用赢得矩阵表示(表1)。

表1 对策赢得矩阵

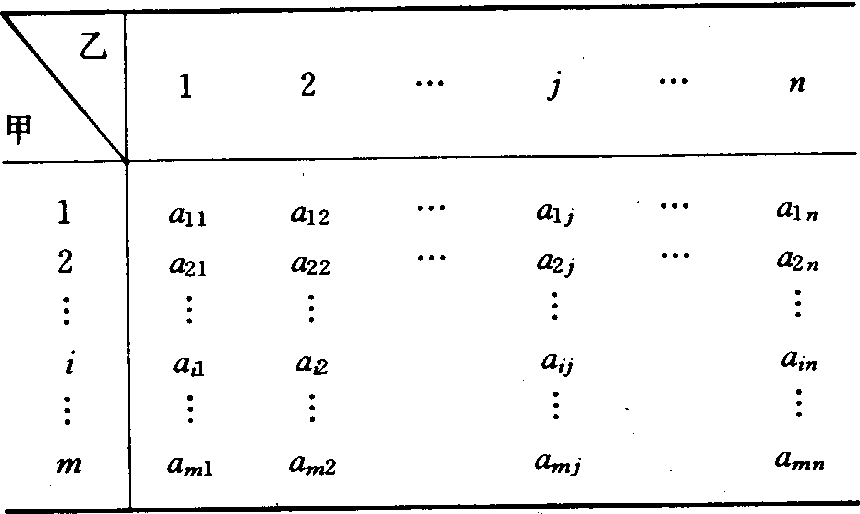
矩阵中a_ij为一方的（例如甲）赢得值。当甲取策略i，乙取策略j时，甲之得为a_ij，而乙之得为-a_ij，故a_ij+(-a_ij) =0，称为二人零和对策。
二人零和对策还可分为纯策略解与混合策略解。❶纯策略解。双方规定不管对方采取什么方案，各方总是采用一种方案。例如，假定局中人甲有两个行动方案a₁和a₂，局中人乙也有两个行动方案b₁和b₂可供选择。二人对局构成一个赢得矩阵。矩阵中的赢得值表示甲赢得乙的钱数。这类问题可以根据最大最小理论用悲观准则求解。如表2所示。

表2 纯策略求解过程 (单位：元)

甲 乙	b1	b2	行最小值
a1 a2 列最大值	200* 100 200*	250 300 300	200* 100

注：*表示甲、乙双方对策方案。

在本例中甲如果选a₁，最少能赢得200元，如选a₂，最少能赢得100元。按小、中取大准则选a₁，至少赢得200元。对于乙方，他希望损失最小，因此乙如选b₁最多付出200元，如选b₂，最多付出300元。按大中取小准则选方案b₁，至多付出200元。最终结果是甲选a₁，乙选b₁，对策解为200元。此值恰等于行最小值中的最大值和列最大值中的最小值，称为鞍点。这种对应于鞍点的策略，称为最优纯策略。
❷混合策略解。如果在二人零和对策中找不到一个双方都满意的可重复采用的策略，就成为无鞍点的二人零和对策，此时必须采用混合策略求解，即在重复对策时各方必须交替采用不同方案。例如，甲、乙两公司在推销产品的活动中，甲公司采取a₁和a₂两种方案，乙公司采取b₁和b₂两种方案，构成赢得矩阵。矩阵中的赢得值表示市场占有率(%)。正值表示甲赢得而乙失去的值，负值表示甲失去而乙赢得的值。假定用悲观准则求解，如表3，结果是甲选a₁，乙选b₂。没有鞍点。这种情况下双方不能重复采用一种方案，而必须采取混合策略。例如，甲先选a₁，乙将选b₂。当甲发现乙选b₂时，甲将转向a₂，这样甲将获得比a₁大的赢得值。当乙发现甲转向a₂，必然转而选b₁，于是甲又将转向a₁，等等，双方将会发现，改变方案比总是采用一种方案要好。平均赢得值由双方采用各方案的次数比例决定，而且在某一比例时对各方都是最好的。本例的最终结果：甲公司选a₁、a₂的次数比为3:5；乙公司选b₁、b₂的次数比为1:3，甲的期望赢得值为1/4，乙的期望失去值也为1/4。局中人数m=2和方案数n=2的混合策略对策问题可用解析法或图解法求解，m≥2, n≥2的有限对策问题，可用线性规划法求解。

表3 混合策略对策问题

甲 乙	b1	b2	行最小值
a1 a2 列最大值	4 -2 4	-1* 1* 1*	-1* -2

非零和对策 在非零和对策中，局中人一方赢得的值不等于另一方失去的值。这意味着在环境中，某些参与者可能分担得失。所以非零和对策不是严格的竞争，因而具有合作的可能性，这样就使对策问题的求解过程变得更复杂，更不确定。因为在非零和对策中出现了心理状态、信息交流、讨价还价等行为因素，可能妨碍用数学方法来获得一个简单合理的解。所以非零和对策只能根据具体参加者的个人情况和需求来求解。
N人对策 N>2时对策的主要特点之一是联盟。局中人之间的关系逐渐稳定，成为两个对抗集团。这种情况下可以按二人对策问题求解。
微分对策 是连续时间的多阶段对策。状态转移可用微分方程描述。