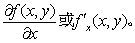导数daoshu
是微分学的基本概念之一。设函数y=f (x)在点x0的某个邻域内有定义，当自变量x在x0处有改变量Δx时，函数相应的改变量为Δy=f (x0+Δx) -f (x0)。若极限
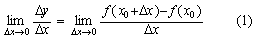
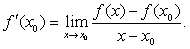
若函数f (x)在开区间(a,b)内的每一点都可导，则称函数f (x) 在开区间 (a,b) 内可导。
若函数f (X)在开区间 (n,b) 内可导，则f (x)在点x0处的导数由x0唯一确定，所以f (x)的导数仍是x的函数，称为f (x) 的导函数，记作f′ (x)。
函数的导数值f′ (x0)反映了函数f (x)在点x0附近变化的快慢程度。导数在实际问题中有着广泛的应用。
例如，运动的瞬时速度v (t)是路程s (t)对时间t的导数，即v (t ) =s ′ (t)。
又如，电流强度i (t)是电量Q (t)对时间t的导数，即i (t) =Q ′ (t)。
在微积分产生之初，导数概念就是从不同角度引出的。牛顿从研究运动的瞬时速度问题入手，引出导数概念(1687年)，莱布尼兹则是由研究曲线的切线问题而引出导数概念的 (1684年)。
导数
又称“微商”。设一元函数y=f(x)，当自变量从x变化到x+△x，函数值从f(x)变化到f(x+△x)时，函数值的增量与自变量增量比值的极限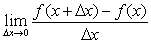
若是存在，则称此极限为f(x)在x的导数。记为f′(x)或dy/dx。研究多元函数导数时，考虑函数对某一变元的变化率。例如设二元函数f(x,y)，如果x的变增量为△x，函数值有增量f(x+△x,y)-f(x,y)；当此增量与△x的比值极限存在，就称函数对x的偏导数存在。记作