平均数pingjunshu
使用最广泛、最普通的一科集中量数。包括算术平均数、几何平均数和倒数平均数。
算术平均数 通常简称为平均数。是一群数据的总和、除以数据个数所得的商,即![]()
式中 ——算术平均数
N——数据总个数
Xi——第i个数据,i=1、2,…,N
[例1] 某小组10个学生的语文测验成绩为78、62、84、90、72、76、83、95、77、78,则其算术平均数为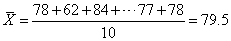
若一群数据可分成若干部分,各部分的数据个数分别为N1,N2,…,NK,各部分的算术平均数分别为1,2,…,K,则整群数据的算术平均数为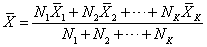
式中的N1,N2,…,NK一般是不等的,若把它们视为![]()
各部分的数据个数不同或权数不同时,要用上式来计算全体的算术平均数。
[例2] 某年级各班一次英语考试成绩如下:
| 班别 | 一 | 二 | 三 | 四 | 五 |
| 人数 | 30 | 40 | 50 | 48 | 52 |
| 平均分 | 80 | 80 | 65 | 65 | 60 |
全年级的总平均分为:
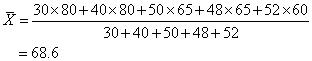
在已分组的次数分布表中,可用下式求算术平均数:
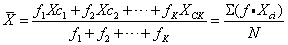 式中 f——各组的次数
式中 f——各组的次数Xci——各组的组中点,i=1,2,…,k
如根据“次数分布表”条中的数据,可计得算术平均数为
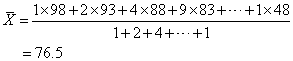
用此式计得的算术平均数与真实平均数(76.4)非常接近。
算术平均数在几何上或物理上表示一群数据的中心或重心位置。它可用于各群(组)数据之间的比较。但它易受数据中的极端值的影响,从而减弱它作为集中量数的代表性。
几何平均数 是一组数据(设有N个)连乘积的N次方根,即
若数据较多或较大时,可用取对数的方法来求几何平均数,即
几何平均数实际上是各数据对数的算术平均数,适用于计算具有递增(减)性数据的集中量数。如2、6、18、54、162为等比级数(公比为3),若求这5个数据的集中量数,则不宜用算术平均数,而应用几何平均数,因为前者(=48.4)在本数列中并不居中,而后者(G=18)恰为居中。
[例3] 1980~1983年我国职业中学的在校学生数如下。求这4年在校学生的平均数与年平均增长率。
| 年份 | 1980 | 1981 | 1982 | 1983 |
| 人数 (万人) | 13.3 | 21.3 | 35.7 | 53.9 |
显然,这是一组具有递增性的数据,故宜用几何平均数。
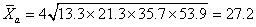
为求年平均增长率,需先求出以前一数据为基础的逐年增长率,即:21.3÷13.3=1.60,35.7÷21.3=1.68,53.9÷35.7=1.51;然后求出这三个比率的平均值,即
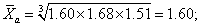
由于
还包括着以第一年的数据为基数的1,因而必须减去1,即:1.60-1=0.60。故后三年的年平均增长率约为60%。
倒数平均数 亦称调和平均数。是一组数据的倒数的算术平均数之倒数,计算公式为:
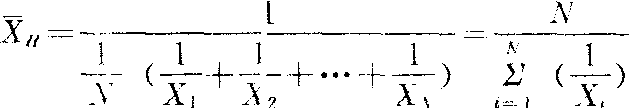
倒数平均数适用于解决平均速度一类性质的问题。
[例4] 设甲、乙、丙3个学生的解题速度如下:甲生每小时8题、乙生每小时5题、丙生每小时4题。求3人的平均解题速度?
由于此例是求平均速度问题,故应用倒数平均数。
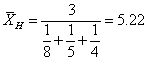
验算:由于甲生解1题所花的时间为1/8,即0.125小时、乙生所花的时间为1/5=0.2小时,丙生所花的时间为1/4=0.25小时,则他们各解1题(共解3题)所花费时间为0.575小时;根据倒数平均数,他们在0.575小时应解题数为0.575×5.22=3 (题),与事实相符。(如果是算术平均数=5.7,则在0.575小时内他们应解题数为0.575×5.7=3.3 (题),与事实不符;几何平均数
 =5.4,也与事实不符)。
=5.4,也与事实不符)。平均数Pingjunshu
使用最广泛的一种表示数据集中趋势的量数。包括算术平均数、加权平均数、几何平均数和调和平均数。算术平均数:是一组数据的总和除以数据个数所得的商。通常简称为平均数,计算公式为:
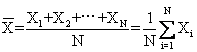
 ——算术平均数;N——数据个数;Xi——第i个数据,i=1,2,…,N。加权平均数:是一组数据中各数据与其权重之积的总和除以各权重总和所得的商,即
——算术平均数;N——数据个数;Xi——第i个数据,i=1,2,…,N。加权平均数:是一组数据中各数据与其权重之积的总和除以各权重总和所得的商,即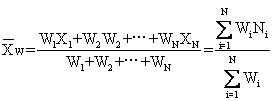
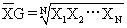
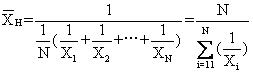
平均数
又称“平均指标”。指在同质总体内,按某一数量标志说明该总体在一定历史条件下的一般水平的综合指标。如平均人数、平均工资等。
平均数mean
反映统计研究对象某一数量标志的典型水平或代表性水平的数值。它的特点是把总体单位的数量标志值的个别差异抽象化,反映了变量值的集中趋势。平均数只能用于同类现象,并要以大量观察的资料为依据。平均数的表现形式有算术平均数、几何平均数、平方平均数、调和平均数等。