平面的基本性质pingmian de jiben xingzhi

平面有下面三个基本性质，一般把它当作公理.
公理1 若一条直线上的两点在一个平面内，则这条直线上所有的点都在这个平面内(图1).

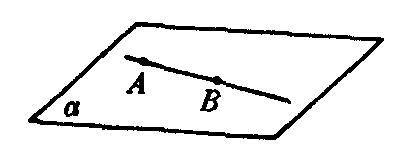
图1

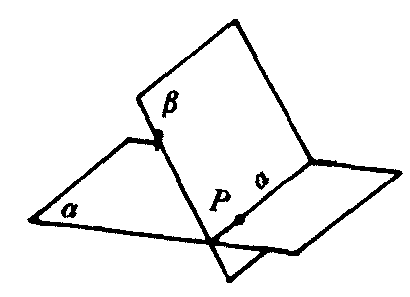
图2

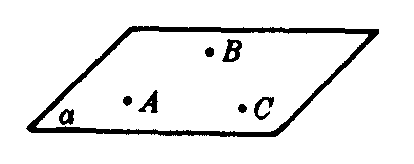
图3

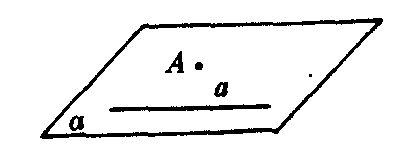
图4

公理2 若两个平面有一个公共点，则它们有且只有一条通过这个点的公共直线(图2).
公理3 经过不在同一条直线上的三点，有且只有一个平面(图3).
以上三条公理和平面几何公理合在一起，构成了中学阶段立体几何的一个较完备的公理系统，为研究空间图形打下了基础.根据上述公理，可以得出下面的推论：
推论1 经过一条直线和这条直线外的一点，有且只有一个平面(图4).
推论2 经过两条相交直线，有且只有一个平面(图5).
推论3 经过两条平行直线，有且只有一个平面(图6).

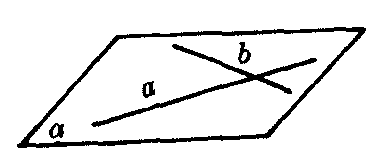
图5

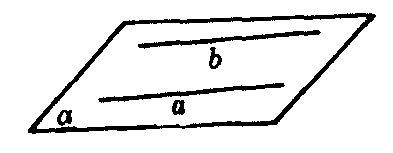
图6

平面的基本性质是研究空间图形的理论基础.
公理1的作用有：❶借助于直线的无限伸展性刻划了平面的无限伸展性.
❷利用了直线的“直”，刻划了平面的“平” (即任何方向上的“直”就是所谓的“平”).
❸是判定直线在平面内的依据.即要证明一条直线在某一平面内，必须且只须证明这条直线上有两个点在此平面内.
公理2的作用有：❶从另一角度利用了直线的无限伸展性刻划了平面的无限伸展性，利用了直线的“直”刻划了平面的“平”.
❷是判定两个平面相交的依据.即要证明两个平面相交，必须且只须证明这两个平面有一个公共点.
❸是证明点在直线上的依据.即要证明一个点在某条直线上，可证该点是某两个平面的公共点，而该直线是这两个平面的交线.
❹是证明几点共线的依据.即要证明几点共线，可证这几个点都是某两个平面的公共点.
公理3及三条推论的作用有：❶肯定了空间内平面的存在性.
❷指出了确定平面的条件.
❸是空间内作平面的依据.
❹是证明两个平面重合的依据.即要证明两个平面重合，可证明两个平面有三个不共线的公共点；也可证明两个平面有一个公共点和一条不过此点的公共直线；或证明这两个平面有两条相交的（或平行的）公共直线.