微分weifen
是微积分的重要概念之一。设函数y=f (x)在点x0的某个邻域内有定义。若函数y=f(x) 在点x0的改变量Δy可以表示为
Δy =AΔx +o(Δx), (1)
其中A与Δx无关而与x0有关,则称函数f (x)在点x0可微,ΔAx称为函数f (x)在点x0的微分,记作dy |x=x0= AΔx。微分具有以下两个特点:
❶ dy=AΔx是Δx的线性函数,表达式简单。
❷ Δy-dy=o (Δx),即Δy与dy相差一个比Δx高阶的无穷小量。换言之,用微分代替改变量,当|Δx|充分小时,不仅误差|Δy-dy|本身很小,更重要的是,其相对误差|(Δy-dy)/AΔx|可以任意小。所以,在式(1)右端,AΔx起主要作用。
上述的两个特点表明,微分dy是Δy的既简单而又具有一定精确度的近似表达式。
函数f(x)在点x0可微的充分必要条件是f(x)在点x0可导,且 (1) 中的A等于f′ (x0)。
这表明,一元函数的可导与可微是等价的。函数y=f (x)在点x0的微分可表示为dy|x=x0= f′ (x0) Δx。
若函数y=f (x)在区间I上的每一点都可微,则称f (x)为I上的可微函数。函数y=f (x)在区间I上的微分记作dy=f′ (x)Δx。d y既依赖于x,又依赖于Δx,而x与Δx是互相独立的两个变量。
通常约定,自变量x的微分dy=Δx。于是,
d y =f′ (x)dx,
从而有
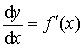 。
。记号dy/dx具有双重意义。作为整体记号,它表示f (x)的导数f′ (x);作为运算记号,它表示函数的微分与自变量微分之比。因此,导数也称为微商。
微分
函数y=f(x)的自变量有一改变量△x,那么函数值对应的改变量△y的近似值f′(x)△x称为y的微分,记为dy=f′(x)dx。f′(x)是f(x)在x点的导数。对多元函数,如二元函数u=f(x,y),若对x和y的偏导数都存在,称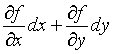 是u在(x,y)点的全微分。记为du。
是u在(x,y)点的全微分。记为du。