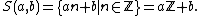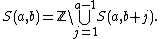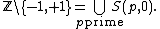1. Furstenberg's proof

2. Notes

3. References

4. External links

In mathematics, particularly in number theory, Hillel Furstenberg's proof of the infinitude of primes is a topological proof that the integers contain infinitely many prime numbers. When examined closely, the proof is less a statement about topology than a statement about certain properties of arithmetic sequences. Unlike Euclid's classical proof, Furstenberg's proof is a proof by contradiction. The proof was published in 1955 in the American Mathematical Monthly while Furstenberg was still an undergraduate student at Yeshiva University.

Furstenberg's proof

Define a topology on the integers Z, called the evenly spaced integer topology, by declaring a subset U ⊆ Z to be an open set if and only if it is either the empty set, ∅, or it is a union of arithmetic sequences S(a, b) (for a ≠ 0), where

In other words, U is open if and only if every x ∈ U admits some non-zero integer a such that S(a, x) ⊆ U. The axioms for a topology are easily verified:

• By definition, ∅ is open; Z is just the sequence S(1, 0), and so is open as well.
• Any union of open sets is open: for any collection of open sets U_i and x in their union U, any of the numbers a_i for which S(a_i, x) ⊆ U_i also shows that S(a_i, x) ⊆ U.
• The intersection of two (and hence finitely many) open sets is open: let U₁ and U₂ be open sets and let x ∈ U₁ ∩ U₂ (with numbers a₁ and a₂ establishing membership). Set a to be the lowest common multiple of a₁ and a₂. Then S(a, x) ⊆ S(a_i, x) ⊆ U_i.

This topology has two notable properties:

1. Since any non-empty open set contains an infinite sequence, a finite set cannot be open; put another way, the complement of a finite set cannot be a closed set.
2. The basis sets S(a, b) are both open and closed: they are open by definition, and we can write S(a, b) as the complement of an open set as follows:

The only integers that are not integer multiples of prime numbers are −1 and +1, i.e.

By the first property, the set on the left-hand side cannot be closed. On the other hand, by the second property, the sets S(p, 0) are closed. So, if there were only finitely many prime numbers, then the set on the right-hand side would be a finite union of closed sets, and hence closed. This would be a contradiction, so there must be infinitely many prime numbers.

Notes

References

• {{Cite document | last1=Aigner | first1=Martin|author1-link=Martin Aigner | last2=Ziegler | first2=Günter M. | author2-link=Günter M. Ziegler | title=Proofs from The Book | publisher=Springer-Verlag | location=Berlin, New York | year=1998 | postscript=| title-link=Proofs from The Book}}
• {{cite journal

• {{Cite journal

• {{Cite journal

External links

• Furstenberg's proof that there are infinitely many prime numbers at Everything2
• {{PlanetMath|urlname=FurstenbergsProofOfTheInfinitudeOfPrimes|title=Fürstenberg's proof of the infinitude of primes}}

• 1481 BC
• 1481 in literature
• 1482
• (148209) 2000 CR105
• 1482 BC
• 1482 in literature
• 1483
• 1483 BC
• 1483 in literature
• 1484
• 1484 BC
• 1484 in literature
• 1485
• 1485 BC
• 1485 in literature
• 1486
• 1486 BC
• 1486 in literature
• 1487
• 1487 BC
• 1487 in literature
• 1488
• 14 88
• 1488 BC
• 1488 in literature