最小二乘法zuixiao erchengfa
19世纪初，著名数学家高斯和P. S. 拉普拉斯由于研究误差分析而引进了最小二乘法，这个方法经过A. A.马尔可夫等许多学者的发展，成为统计分析上一个极为重要的方法。
最小二乘法原理如下：
设y是变量x1 ,x2 ，…，xn的函数，含有k个参数a1,a2，“ …，ak。即
y =f(a1,a2，…，ak;x1,x2，…，xm)。
今对y和x1,x2，…，xm作n次观测得(x1i,x 2i，…，xmi;y i) (i=1, 2, …， n)，于是y的理论值
＝f (a1 ,a2 ，…，ak; x1i,x 2i，…，xmi)与观察值yi的绝对误差为|yi-
i| (i=1, 2，…， n)，式中有绝对值记号，不便于进一步分析讨论，由于任何实数的平方都是正数或零，因此，可以要求上面n个误差在平方和最小的意义下，使得函数y=f (a1,a2，…，ak ; xi1 ,xi2，…，xim)与观测值y1,y2，…，y n最佳拟合，也就是参数a1 ,a2，…，ak应使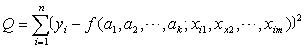
=最小值
由微分学的求极值方法可知a1,a2 ，…，ak应满足下列方程组
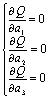
这种根据偏差的平方和为最小的条件来选择参数a 1,a 2 ，…，a k的方法叫做最小二乘法。
最小二乘法
一种常用的数学方法。在实验中获得了自变量与因变量的若干个数对(x1,y1),(x2,y2)，…，(xn,yn)，要找出一个已知类型的函数y=f(x)(如线性函数y=ax+b等)，使得偏差平分和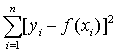
最小。 常用于工程技术和科学研究的数据处理。
最小二乘法
考虑一个简单的例子。对x的一系列选定值x1,x2，…，xn，测出了y的相应值y1,y2，…，yn, 且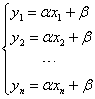
现要求出α和β的最佳值满足以上线性方程组。设ηi=yi—(αxi+β)，利用
最小而求出α和β使xi和yi最大限度地满足y=αx+β，这个近似表达式叫经验公式，这种根据偏差ηi的平方和为最小的条件来选择常数α和β的方法，叫最小二乘法。对上例，利用函数的极值条件有：
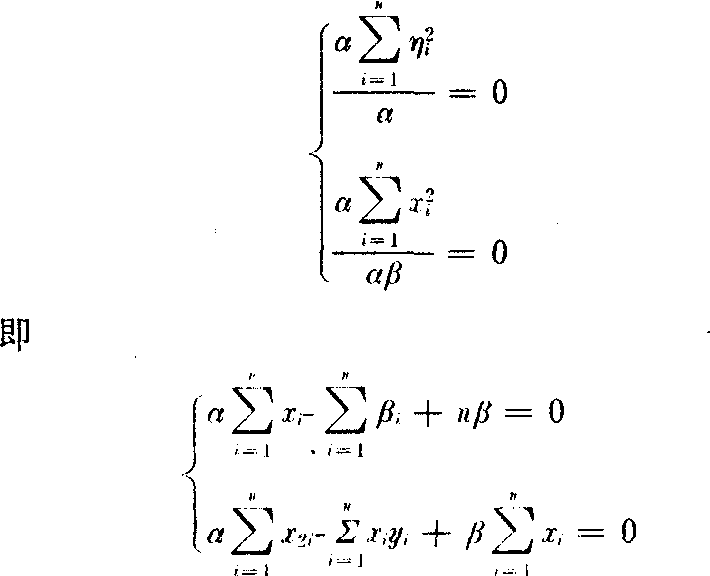
由此求出α和β。经验表明，在一般情况下，这样确定的经验公式可以很好地拟合给定的数据。最小二乘法是由勒让德提出的，在实践中应用广泛。