正态分布zhengtai fenbu

指一种两头小、中间大而隆起、两边对称并呈“钟形”的特定概率分布，其数学表达式为

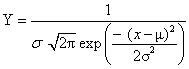
式中 Y——频率（相对次数）
μ——总体平均数
σ——总体标准差
x——随机变量
π——常数(约为3.14159)
exp——常数(约为2.71828)
从式中可见：正态分布曲线是由μ和σ所决定的；当μ与σ不同时，就有不同的正态分布曲线。若用z=x-μ/σ代入上式，即平均数为0、标准差为1时，则变为

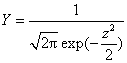
这就是标准正态分布。也就是我们通常所说的正态分布，其Y值可从正态曲线的纵线表中查到。
正态分布曲线有下列性质：❶曲线以z=0为中心，两边也对称；
❷曲线在z=0处有最大的频率(Y=＝0.3989);
❸曲线在z=±1处有两个拐点；
❹曲线下面的面积为1;
❺曲线两端向基线无限延长、接近基线，但永远不与基线相交。
正态分布下的面积与μ、σ有下列关系：以平均数为中心向两边各取1个标准差(即μ±σ)，其范围约占总面积的68.26%；若向两边各取2个标准差(即μ±2σ)，则其范围约占总面积的95.45%；若向两边各取3个标准差(即μ±3σ)，则其范围约占总面积的99.73%。

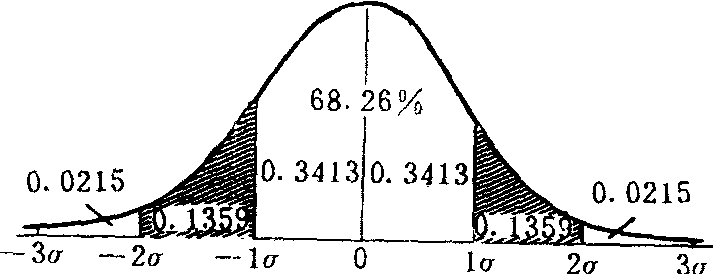
正态曲线下不同σ单位之间占总面积的比例

正态分布在数理统计中是最重要的一种分布。由于教育与心理上许多现象(如学习成绩、智力水平、身高体重、感觉阈限等)的数据分布服从或近似服从正态分布，因而它在教育研究中有极重要的地位和广泛的应用。

正态分布zhengtai fenbu

设连续型随机变量X的概率密度为

其中μ,σ> 0为常数，则称X服从参数为μ,σ的正态分布，记作X ～N (μ,σ²)。正态分布的分布函数为

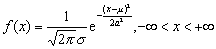
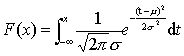
若一个随机变量X的分布函数是正态分布，也称X是一个正态变量。
正态分布是概率论中最重要的一个分布，德国数学家高斯在研究误差理论时曾用它来刻划误差，因而在许多场合也把此分布称为高斯分布。许多实际问题中的变量，如测量误差、射出时弹着点与靶心的距离、热力学中理想气体的分子速度、某地区成年男子身高等，经验表明都服从正态分布。由理论研究表明，若一个变量受到大量微小的、独立的随机因素的影响，则这个变量一般是正态变量。
正态分布的概率密度函数具有下列性质：
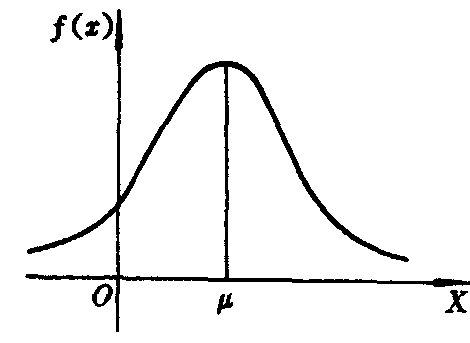
❶在直角坐标系内，f (x)的图形呈钟型，以X轴为水平渐近线。

❷密度分布曲线关于直线x=μ对称，即

f (μ+x) =f (μ-x)。

❸在x=μ时，取到最大值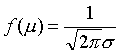在x=μ±σ处图象有拐点。

❹若σ固定，改变μ的值，则f (x)的图形沿着X轴移动，而不改变其形状。若μ固定，改变σ的值，由式子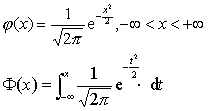可知，σ越小时，图形变得越陡，因而X落在μ处附近的概率越大；反之，当σ的值增大时，曲线将变得平坦。
正态分布的概率密度f (x)与分布函数F (x)的图形如下。

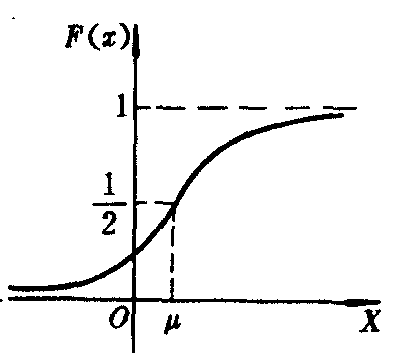
正态分布zheng tai fenbu

又称常态分布、高斯分布。随机变量的一种重要的、应用最多的分布。其数学公式为：

式中e为自然对数的底，μ为平均值，σ为标准差，x为随机变量的取值。最初为德·毛佛尔(De·Moivne)发现，德国数学家高斯(C.F.Gauss)等对其推导做过很大贡献。正态分布曲线有以下特点：曲线呈钟形且左右对称，拐点在μ±σ处，曲线与横坐标所包围的面积为1。曲线随σ大小变化，当μ=0,σ=1时，正态曲线高度适中，称标准正态分布。当σ<1时，曲线高狭，当σ>1时，曲线低阔。有编制好的正态分布表供应用。

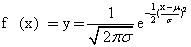
正态分布Zhengtai fenbu

一种重要的连续型随机变量的概率分布，其数学表达式为

式中 π是圆周率3.14159…； e是自然对数的底2.71828…；x为随机变量取值，-∞

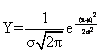
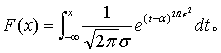
正态分布

又称“高斯分布”、“常态分布”。是一种连续型随机变量的分布。如果随机变量X的概率密度函数为：

则称X服从参数为μ与σ的正态分布，记为X~N(μ,σ²)。在概率论与数理统计的各种分布中居于首要地位。常被应用于测验分数统计中。

正态分布normal distribution

连续性变数的一种最主要的理论分布。它是二项分布的极限形式。如果随机变量ξ的概率密度为：

则称ξ服从正态分布N(μ,σ²)。正态分布曲线以算术平均数μ为原点，方差为σ²，向左右两侧作对称分布，并以x轴为渐近线。其多数次数集中在μ附近；离平均数愈远，分布次数愈少，呈中间高两头低的钟形曲线。算术平均数、中数和众数在|x=μ|=1σ处有拐点。它以参数μ和σ的不同而表现为一系列曲线，与x轴之间的总面积等于1。曲线上任意区间的面积等于x落于这个区间内的概率。μ=0,σ²＝1的正态分布，即N(0,1)，称为标准正态分布。