点到平面的距离dian daopingmian de juli

指从平面外一点引一个平面的垂线，这个点和垂足间的距离.

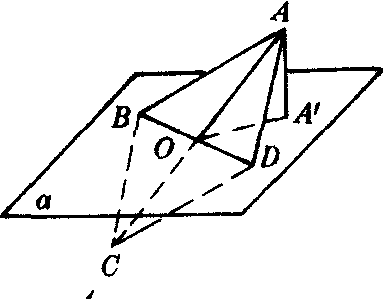
图1

求点到平面的距离的计算题是常见的题目，同时它又是平行的直线和平面，两平行的平面间的距离的计算的基础.求点到平面的距离，常采用以下方法：
❶直接利用定义求.
例如图1，已知平面α过平行四边形ABCD的对角线BD，且AC=20cm,AC与平面α成30°角，求A点到平面α的距离.
解 过A作AA′⊥α垂足为A′.设AC∩BD=O，连结A′O，则∠AOA′=30°.所以AA′=OA·sin30°=5cm.因此，点A到α的距离为5cm.

❷利用两平面互相垂直的性质，即如果已知点在已知平面的垂面上，则已知点到两平面交线的距离就是所求的点到平面的距离.
例 如图2，过圆锥SO的顶点作截面SAB，使截面和底面成60°的二面角，截面截底面圆O的弧为120°，若这截面的面积为24cm²，求底面圆心到截面SAB的距离.

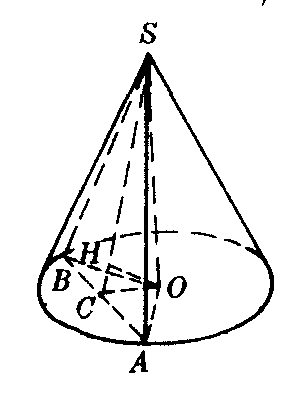
图2

解 过O作OC⊥AB于C.连结SC. 由三垂线定理可知SC⊥AB，因此AB⊥平面SCO.因为AB⊂截面SAB，所以截面SAB⊥平面SCO，且平面SAB∩平面SCO=SC.在平面SCO内过O作OH⊥SC于H，则OH⊥平面SAB.设

OH=h, 则

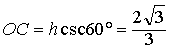
h. 连结OA, 则∠AOC=60°. 在Rt△AOC中， AC=OC

·tg60°=2h.

在Rt△SCO中，

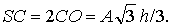
因

为截面SAB的面积

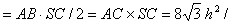
3,

所以，

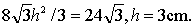
也就是圆心

O到截面SAB的距离为3cm.

❸利用锥体的体积计算.

例如上面题目中，不难算出

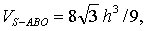
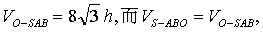
所以

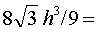
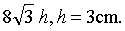
❹通过特殊图形的性质求.如求正三棱锥的顶点到底面的距离，只要求出顶点到底面中心的距离就可以了.