直线和平面垂直的判定定理zhixian he pingmianchuizhi de panding dingli

定理1 若一条直线和一个平面内的两条相交直线都垂直，则这条直线就垂直于这个平面.

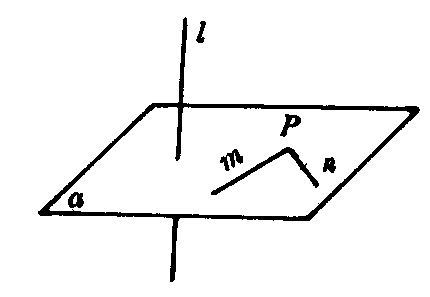
图1

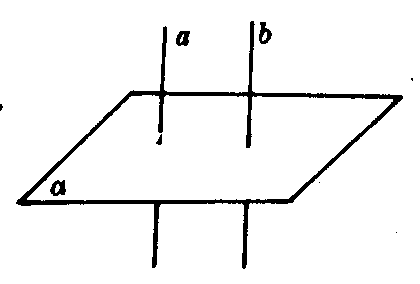
图2

如图1 若m⊂a,n⊂a,m∩n=P,l⊥m,l⊥n，则l⊥a.
定理2 若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面.
如图2，若a∥b,a⊥a，则b⊥a.
定理1中两条直线是相交直线，这个条件是必要的.因为一条直线和一个平面内的两条平行线都垂直，这条直线并不一定和这个平面垂直.
上述定理的主要作用是：❶判定直线和平面垂直.
❷证明两直线互相垂直.如要证明直线a和b垂直，可证a 垂直于b所在的某个平面内的两条相交直线.

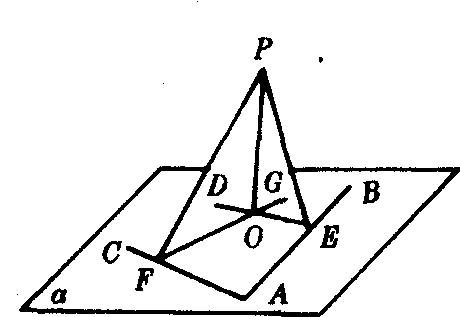
图3

例 如图3，已知Pα,AB,AC⊂α,PE⊥AB,PF⊥AC,E,F分别为垂足.DE⊥AB,FG⊥AC,DE∩FG=O.求证PO⊥α.
证 因为AB⊥PE,AB⊥DE,PE∩DE=E，所以AB⊥平面POE.因为PO⊂平面POE，所以AB⊥PO.同理可证AC⊥平面POF,AC⊥PO.又因为AB,AC⊂α,AB∩AC=A. 所以PO⊥α.