空间直线方程的各种形式kongjian zhixian fangcheng degvzhong xingshi
❶普遍式 直线的普遍方程又称直线的一般方程。若过直线l的两个不重合的平面方程为a1x+ b1y+ c1z+ d1=0,a2x + b2y+ c2z+ d2 = 0,则直线l可表示为
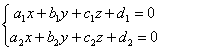
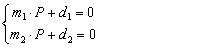
❷投射式 用把直线投射到坐标面上的两个投射面的方程联立表示直线的方程,称为直线的投射方程或投影方程。例如,若x=pz+g是将直线l投影到ZX面上的投射面方程,y=rz+s是将直线l投影到YZ面上的投射面方程,则
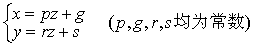 (p,g,r,s均为常数)
(p,g,r,s均为常数)
❸参数式:过定点P0(x0,y0,z0)且与非零常向量S= {l,m,n}平行的直线,它的方程的向量形式是P=P0+ tS (-∞
❹对称式 直线的对称式方程又称直线的标准方程。过P0 (z0,y0,z0)而以l,m,n为一组方向数的直线方
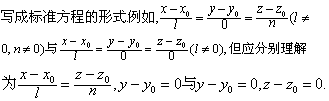 程是,式中x,y,z为直线上任意一点的坐标,这个方程称为直线的对称式方程。它表示过已知点P0 (z0 ,y0 ,z0)且与非零向量{l,m,n,}平行的一条直线。注意:当l,m,n中有一个或两个为零时,仍可写成标准方程的形式。例如,
程是,式中x,y,z为直线上任意一点的坐标,这个方程称为直线的对称式方程。它表示过已知点P0 (z0 ,y0 ,z0)且与非零向量{l,m,n,}平行的一条直线。注意:当l,m,n中有一个或两个为零时,仍可写成标准方程的形式。例如,
| 0,n≠0) |
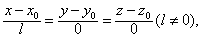 但应分别理解为
但应分别理解为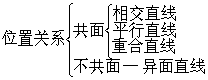 y-y0=0与y-y0=0,z-z0=0。
y-y0=0与y-y0=0,z-z0=0。❺两点式 设已知直线上两个不重合的已知点Pi (x1,y1,z1),P2(x2,y2,z2),则直线的两点式方程为
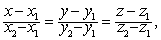 式中,x,y,z为直线上任意一点的坐标。
式中,x,y,z为直线上任意一点的坐标。