中心极限定理zhongxin jixian dingli
为了阐明在何种条件下随机变量之和的分布接近于正态分布，或者说，在何种条件下，随机变量之和的分布可以转化为正态分布，在概率论中，把这一系列定理称之为中心极限定理，常见的中心定理有以下几个：
棣莫佛-拉普拉斯定理 在n重贝努利试验中，事件A在每次试验中出现的概率为p (0
A为n次试验中事件A出现的次数，则
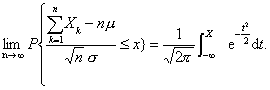
同分布的中心极限定理 设随机变量X k (k=1,2，…)相互独立，服从同一分布，且具有有限的数学期望和方差E (Xk )=μ,D (Xk) =σ2≠0 (t=1,2，…)，则对任意的x有
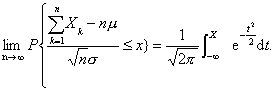
这两个定理反映了在客观实际中有些随机变量，它们是由大量的相互独立的每个的作用又很微小的随机因素的综合影响而成的，这种随机变量往往近似服从正态分布。
中心极限定理
概率论中基本的定律之一。是统计估计的理论基础。内容是：当随机变量具有有限的数学期望和方差时，只要样本容量充分大，从总体中抽取的随机样本平均数就近似地服从正态分布，且样本平均数等于总体平均数。
中心极限定理
在一定条件下断定随着项数的增加，标准化随机变量的和服从标准正态分布的定理的总称。常被应用于测验分数统计中。
中心极限定理central limit theorem
抽样估计中说明随机变量的分布是正态或近似正态的一种理论。由法国数学家德·莫威尔(De Moivre)于1733年首次提出，1901年由李雅普诺夫(Liapounov)在一般条件下推导出此定理，1920年由卜里耶(Polya)第一次正式命名，并为数理统计学界采用。定理认为：当随机变量具有有限的数学期望和方差时，只要样本容量充分大，从总体中随机地抽取样本，其样本平均数的分布就近似地服从正态分布；样本平均数的期望就等于总体平均数；样本平均数的标准差就等于总体标准差的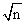
分之一。中心极限定理的数学表达式之一为：
