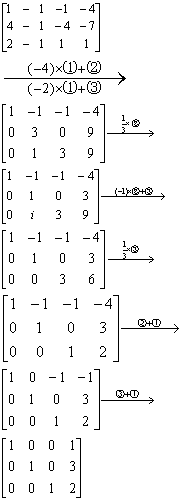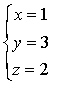高斯消去法gaosi xiaoqufa

解线性方程组的一种重要方法.也称之为消元法.这种方法有比较严格的程序，它分为以下两个步骤
❶顺序消元.
设方程组为

式中a_ij(i,j=1,2，…，n)和c₁,c₂，…，c_n都是已知数，且系数行列式D≠0.
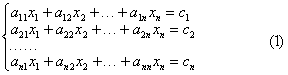
不妨假定a₁₁≠0，先以1/a₁₁乘以第一个方程，把x₁的系数化为1，然后分别乘以-a₂₁,-a₃₁，…，-a_n1加到第2至第n个方程上，消去后n-1个方程中的x₁，将方程组化为

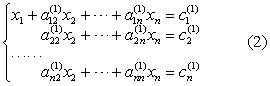
不妨设(2)中a⁽¹⁾₂₂≠0，用同样的方法把第二个方程中x₂的系数化为1，并消去后n-2个方程中的x₂.这样继续下去，最后得到

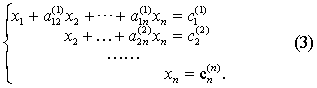
❷回代求解.
在完成第一个步骤的基础上，按相反顺序逐个消去方程组(3)中的第n-1个方程中的x_n；第n-2个方程中的x_n,x_n-1；…；第一个方程中的x_n,x_n-1…，x₂，得到

这就是方程组的解.
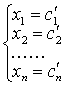
方程组
(1)中未知数的所有系数组成一个系数矩阵.

所有的常数项也组成一个常数项矩阵

把系数矩阵和常数项矩阵合在一起组成一个增广矩阵

只要运用矩阵的初等变换，把方程组的增广矩阵变换为

就可求得方程组(1)的解为

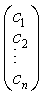
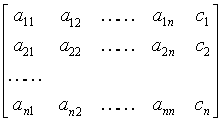
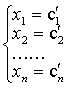
例 解方程组

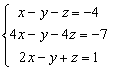
解 方程组的增广矩阵为

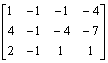
设❶,
❷,
❸分别为矩阵的第一、二、三行.现在对矩阵作初等变换.

所以原方程组的解为