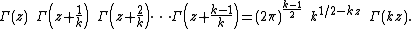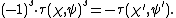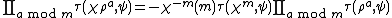“Hasse–Davenport relation”的意思、由来-开放百科全书

词条

Hasse–Davenport relation

释义

Hasse–Davenport lifting relation
Hasse–Davenport product relation
References

The Hasse–Davenport relations, introduced by {{harvs|txt|author2-link=Helmut Hasse|last2=Hasse|author1-link=Harold Davenport|last1=Davenport|year=1935}}, are two related identities for Gauss sums, one called the Hasse–Davenport lifting relation, and the other called the Hasse–Davenport product relation. The Hasse–Davenport lifting relation is an equality in number theory relating Gauss sums over different fields. {{harvtxt|Weil|1949}} used it to calculate the zeta function of a Fermat hypersurface over a finite field, which motivated the Weil conjectures.

Gauss sums are analogues of the gamma function over finite fields, and the Hasse–Davenport product relation is the analogue of Gauss's multiplication formula

In fact the Hasse–Davenport product relation follows from the analogous multiplication formula for p-adic gamma functions together with the Gross–Koblitz formula of {{harvtxt|Gross|Koblitz|1979}}.

Hasse–Davenport lifting relation

Let F be a finite field with q elements, and F_s be the field such that [F_s:F] = s, that is, s is the dimension of the vector space F_s over F.

Let be an element of .

Let be a multiplicative character from F to the complex numbers.

Let 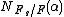be the norm from to defined by

Let

be the multiplicative character on which is the composition of with the norm from F_s to F, that is

Let ψ be some nontrivial additive character of F, and let

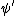be the additive character on which is the composition of with the trace from F_s to F, that is

Let

be the Gauss sum over F, and let

be the Gauss sum over .

Then the Hasse–Davenport lifting relation states that

Hasse–Davenport product relation

The Hasse–Davenport product relation states that

where ρ is a multiplicative character of exact order m dividing q–1 and χ is any multiplicative character and ψ is a non-trivial additive character.

References

{{Citation | last1=Davenport | first1=Harold | last2=Hasse | first2=Helmut | title=Die Nullstellen der Kongruenzzetafunktionen in gewissen zyklischen Fällen. (On the zeros of the congruence zeta-functions in some cyclic cases) | url=http://resolver.sub.uni-goettingen.de/purl?GDZPPN002173123 | language=German |zbl=0010.33803 | year=1935 | journal=Journal für die Reine und Angewandte Mathematik | issn=0075-4102 | volume=172 | pages=151–182}}
{{Citation | last1=Gross | first1=Benedict H. | last2=Koblitz | first2=Neal | author2-link=Neal Koblitz | title=Gauss sums and the p-adic Γ-function | doi=10.2307/1971226 |mr=534763 | year=1979 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=109 | issue=3 | pages=569–581| jstor=1971226 }}
{{cite book

| last = Ireland
| first = Kenneth
| first2 = Michael |last2=Rosen
| title = A Classical Introduction to Modern Number Theory
| publisher = Springer
| year = 1990
| pages = 158–162
| isbn = 978-0-387-97329-6}}

{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Numbers of solutions of equations in finite fields | doi=10.1090/S0002-9904-1949-09219-4 | mr=0029393 | year=1949 | journal=Bulletin of the American Mathematical Society | issn=0002-9904 | volume=55 | pages=497–508 | issue=5}} Reprinted in Oeuvres Scientifiques/Collected Papers by André Weil {{ISBN|0-387-90330-5}}

1 : Cyclotomic fields

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。