请输入您要查询的百科知识：

　

词条 Membrane curvature
释义

  1. Basic geometry

  2. Lipid spontaneous curvature

  3. Proteins can Induce Curvature

      1. Lipid clustering    2. Rigid scaffold    3. Insertion of hydrophobic protein motifs    4. Protein crowding  

  4. References

Membrane curvature is the geometrical measure or characterization of the curvature of membranes.

The membranes can be naturally occurring or man-made (synthetic). An example of naturally occurring membrane is the lipid bilayer of cells, also known as cellular membranes.[1] Synthetic membranes can be obtained by preparing aqueous solutions of certain lipids. The lipids will then "aggregate" and form various phases and structures. According to the conditions (concentration, temperature, ionic strength of solution, etc.) and the chemical structures of the lipid, different phases will be observed. For instance, the lipid POPC (palmitoyl oleyl phosphatidyl choline) tends to form lamellar vesicles in solution, whereas smaller lipids (lipids with shorter acyl chains, up to 8 carbons in length), such as detergents, will form micelles if the CMC (critical micelle concentration) is reached.

Basic geometry

A biological membrane is commonly described as a two-dimensional surface, which spans a three-dimensional space. So, to describe membrane shape, it is not sufficient to determine the membrane curling that is seen in a single cross-section of the object, because in general there are two curvatures that characterize the shape each point in space. Mathematically, these two curvatures are called the principal curvatures, c1 and c2, and their meaning can be understood by the following thought experiment. If you cross-section the membrane surface at a point under consideration using two planes that are perpendicular to the surface and oriented in two special directions called the principal directions, the principal curvatures are the curvatures of the two lines of intercepts between the planes and the surface which have almost circular shapes in close proximity to the point under consideration. The radii of these two circular fragments, R1 and R2, are called the principal radii of curvature, and their inverse values are referred to as the two principal curvatures.[2]

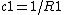
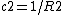
The principal curvatures C1 and C2 can vary arbitrarily and thereby give origin to different geometrical shapes, such as cylinder, plane, sphere and saddle. Analysis of the principal curvature is important, since a number of biological membranes possess shapes that are analogous to these common geometry staples. For instance, prokaryotic cells such as cocci, rods, and spirochette display the shape of a sphere, and the latter two the shape of a cylinder. Erythrocytes, commonly referred to as red blood cells, have the shape of a saddle, although these cells are capable of some shape deformation. The table below lists common geometric shapes and a qualitative analysis of their two principal curvatures.

Shape C1 C2
Plane 0 0
Cylinder + 0
Sphere + +
Saddle + -

Even though often membrane curvature is thought to be a completely spontaneous process, thermodynamically speaking there must be factors actuating as the driving force for curvature to exist. Currently, there are some postulated mechanisms for accepted theories on curvature; nonetheless, undoubtedly two of the major driving forces are lipid composition and proteins embedded and/or bound to membranes.

Lipid spontaneous curvature

Perhaps the most simple and intuitive driving force in membrane curvature is the natural spontaneous curvature exhibited by some lipids. This is because, depending on their chemical structures, lipids tend to curve with a slight spontaneously negative or positive curvature. Lipids such as DOPC (dioleoyl phosphatidyl choline), diacyl glycerol, dioleyl phosphatidylethanolamine (DOPE) and cholesterol exhibit a negative spontaneous curvature.[3] On the other hand, lipids with smaller acyl chain area to polar head group area ratio tend to curve positively, in other words they exhibit positive spontaneous curvature.[4] The table below lists experimentally determined spontaneous curvatures for different lipids in DOPE (dioleyl phosphatidyl ethanolamine).

Lipid Js (nm−1)
Lysophospholipids
L-lyso PC 1/5.8
O-lyso PC 1/3.8
P-lyso PC 1/6.8
L-lyso PE <1/40
O-lyso PE <1/40
S-lyso PE <1/40
Other Lipids
DOPS 1/14.4
DOPC -1/20
PA -1/4.6
DOPE -1/3
Cholesterol -1/2.9
DCG -1/1.3

The energy requirements to generate a cylinder shaped cell from an originally flat membrane can be expressed as

FCyl =πxLxKb(1/R - 2JB)

where L is the length of the cylinder, JB is the difference between the spontaneous curvature, Js, for the lipids in the inner and outer leaflet divided by two, and Kb is the bending modulus of the bilayer.

The radii of membrane cylinders that form in intracellular membrane-transport pathways are typically ~25–30 nm.[5] So, the spontaneous curvature necessary to generate such cylinders equals ~(1/50) nm–1. As JB results from a difference in the spontaneous curvatures of the monolayers, an unusual membrane lipid composition would be required to produce such curvature. The lipids cholesterol, dioleoylphosphatidylethanolamine(DOPE) and diacylglycerol are characterized by strongly negative spontaneous curvatures (figure 1) and therefore have the potential to generate a large membrane curvature. However, even for these lipids, the required JB can be reached only if they are extensively concentrated in the internal monolayer.

Proteins can Induce Curvature

Some biologically occurring lipids do exhibit spontaneous curvature which could explain the shapes of biological membranes. Nevertheless, calculations show that spontaneous lipid curvature alone is either insufficient or would require conditions that are unrealistic to drive the degree of curvature observed in most cells. It is now known that lipid curvature is "aided" by protein structures in order to generate complete cellular curvature.

Currently there are 4 proposed mechanisms to explain protein-mediated membrane bending:

  1. Lipid Clustering
  2. Protein forms rigid scaffold
  3. Insertion of amphipathic domains
  4. Protein Crowding

1. Lipid clustering

Bacterial toxins such as cholera toxin B, shiga toxin B favors binding and thus clustering of certain lipid molecules. The effect of lipid clustering, together with the intrinsic shape of individual lipid molecule, give rise to membrane curvature.

2. Rigid scaffold

A classical example of membrane bending by rigid protein scaffold is clathrin. Clathrin is involved in cellular endocytosis and is sequestrated by specific signaling molecules. Clathrin can attach to adaptor protein complexes on the cellular membrane, and it polymerizes into lattices to drive greater curvature, resulting in endocytosis of a vesicular unit. Coat protein complex I (COP1) and coat protein complex II (COPII) follow similar mechanism in driving membrane curvature.[6] Figure A shows a protein coating that induces curvature. As mentioned above, proteins such as clathrin are recruited to the membrane through signaling molecules and assemble into larger polymeric structures that form a rigid structure which serves as a frame for the membrane. Clathrin binds to its receptors that are present in the membrane.

Another example of protein interactions that directly affect membrane curvature is that of the BAR (Bin, amphiphysin, Rvs’) domain. The BAR domain is present in a large family of proteins. Relative to the cellular lipid bilayer, this domain is rigid and exhibits a "banana" shape. It has been postulated that the positively charged amino acid residues in the concave region of the BAR domain would come into contact with the negatively charged polar head groups of lipids in the bilayer, thus allows the binding process.[3] Upon binding, the membrane's curvature is increased by the rigid domain.[8] Figure B shows bending of membrane by banana-shape like BAR domain.

3. Insertion of hydrophobic protein motifs

Hydrophobic portion of protein can act as "wedge" when inserting into lipid bilayer. Epsin is one example that utilizes this mechanism to drive membrane bending. Epsin has several amphipathic alpha helices that allows it to partition between the hydrophobic core of the membrane and surrounding aqueous, hydrophilic environment. Another interesting characteristic of epsin and other proteins that bind to membranes is the fact that it shows high binding affinity for a fairly common membrane lipid, phosphatidylinositol 4,5-bisphosphate (PI-4,5-P2).[8] Unlike other proteins that simply bend the membrane through sheer rigidity, epsin is a globular soluble protein and thus not rigid. The insertion of its helices into the membrane force the neighboring lipids of the leaflet that has been bound to expand laterally. This displacement of lipids on only one of the leaflets increases the bilayer's curvature. Figure C shows membrane bending by insertion of hydrophobic protein parts into lipid bilayer.4.

The figure to the right illustrates the different mechanisms through which proteins can aid and/or induce membrane curvature. In A, an illustration of a BAR domain present in a number of proteins. The curvature is induced by the very shape of this proteic region. This domain attaches to the lipid bilayer through strong coulombic interactions. This idea is supported by the existence of positively charged amino acid residues in the concave region of the BAR domain.[7] These amino acids would come into contact with the negatively charged polar head groups of lipids in the bilayer. This form phenomenon is also referred to as the "scaffold mechanism".

B shows a protein coating that induces curvature. As mentioned above, proteins such as clathrin are recruited to the membrane through signaling molecules and assemble into larger polymeric structures that form a rigid structure which serves as a frame for the membrane. Clathrin binds to its receptors that are present in the membrane.

C illustrates a slightly different mechanism. In this case, the membrane-bending protein does not exhibit intrinsic rigidity. Instead they are often globular and soluble. The protein epsin is an example. Epsin has an ENTH (epsin N-terminal homology) domain which inserts its amphipathic alpha helix into the membrane. Epsin has high binding affinity for the membrane if PI-4,5-P2 is present.[8]

This figure illustrates membrane bending caused by protein crowding. When a high local concentration of proteins (shown in green) are present on membrane surface (shown in black), membrane curvature can be induced. This hypothesis reasoned that the high protein concentration increases the likelihood of repulsions between proteins, therefore generates steric pressure between proteins. To relieve such pressure, lipid membrane has to bend in order to decrease protein repulsions.

4. Protein crowding

The protein crowding mechanism hypothesizes that proteins can bend membrane without directly perturbing membrane structures like the above mechanisms.[9][10] When a high enough local concentration of protein is present on membrane surface, repulsion between protein molecules on the membrane surface can induce membrane curvature.[11] Although contribution of this mechanism remains unclear, multiple experimental and computation evidences have shown the its potential in bending membrane. A recent study even shows that protein crowding can cause membrane bending and leads to membrane fission.[12][13] These studies suggest that high local protein concentration can overcome the energy barrier to bend lipid membrane, and thus can contribute to membrane bending.{{clear}}

References

1. ^{{cite web |title=Curvy Biology |url=http://www.samuelfurse.com/2011/12/curvy-biology/ |work=The Lipid Chronicles }}
2. ^{{cite book | vauthors = Spivak M | title = A Comprehensive Introduction to Differential Geometry | publisher = Brandeis University | location = Waltham | year = 1970 }}
3. ^1 {{cite journal | vauthors = Martens S, McMahon HT | title = Mechanisms of membrane fusion: disparate players and common principles | journal = Nature Reviews. Molecular Cell Biology | volume = 9 | issue = 7 | pages = 543–56 | date = July 2008 | pmid = 18496517 | doi = 10.1038/nrm2417 }}
4. ^{{cite journal | vauthors = Kamal MM, Mills D, Grzybek M, Howard J | title = Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature | journal = Proceedings of the National Academy of Sciences of the United States of America | volume = 106 | issue = 52 | pages = 22245–50 | date = December 2009 | pmid = 20080790 | pmc = 2797532 | doi = 10.1073/pnas.0907354106 }}
5. ^{{cite journal | vauthors = Polishchuk RS, Polishchuk EV, Marra P, Alberti S, Buccione R, Luini A, Mironov AA | title = Correlative light-electron microscopy reveals the tubular-saccular ultrastructure of carriers operating between Golgi apparatus and plasma membrane | journal = The Journal of Cell Biology | volume = 148 | issue = 1 | pages = 45–58 | date = January 2000 | pmid = 10629217 | pmc = 2156208 | doi = 10.1083/jcb.148.1.45}}
6. ^{{cite journal | vauthors = Prinz WA, Hinshaw JE | title = Membrane-bending proteins | journal = Critical Reviews in Biochemistry and Molecular Biology | volume = 44 | issue = 5 | pages = 278–91 | date = 2009-09-25 | pmid = 19780639 | pmc = 3490495 | doi = 10.1080/10409230903183472 }}
7. ^{{cite journal | vauthors = Zimmerberg J, McLaughlin S | title = Membrane curvature: how BAR domains bend bilayers | journal = Current Biology | volume = 14 | issue = 6 | pages = R250–2 | date = March 2004 | pmid = 15043839 | doi = 10.1016/j.cub.2004.02.060 }}
8. ^1 2 {{cite journal | vauthors = Stahelin RV, Long F, Peter BJ, Murray D, De Camilli P, McMahon HT, Cho W | title = Contrasting membrane interaction mechanisms of AP180 N-terminal homology (ANTH) and epsin N-terminal homology (ENTH) domains | journal = The Journal of Biological Chemistry | volume = 278 | issue = 31 | pages = 28993–9 | date = August 2003 | pmid = 12740367 | doi = 10.1074/jbc.M302865200 }}
9. ^{{cite journal | vauthors = Stachowiak JC, Schmid EM, Ryan CJ, Ann HS, Sasaki DY, Sherman MB, Geissler PL, Fletcher DA, Hayden CC | title = Membrane bending by protein-protein crowding | language = En | journal = Nature Cell Biology | volume = 14 | issue = 9 | pages = 944–9 | date = September 2012 | pmid = 22902598 | doi = 10.1038/ncb2561 }}
10. ^{{cite journal | vauthors = Stachowiak JC, Hayden CC, Sasaki DY | title = Steric confinement of proteins on lipid membranes can drive curvature and tubulation | journal = Proceedings of the National Academy of Sciences of the United States of America | volume = 107 | issue = 17 | pages = 7781–6 | date = April 2010 | pmid = 20385839 | pmc = 2867881 | doi = 10.1073/pnas.0913306107 }}
11. ^{{cite journal | vauthors = Guigas G, Weiss M | title = Effects of protein crowding on membrane systems | journal = Biochimica et Biophysica Acta | volume = 1858 | issue = 10 | pages = 2441–2450 | date = October 2016 | pmid = 26724385 | doi = 10.1016/j.bbamem.2015.12.021 }}
12. ^{{Cite web|url=https://www.bmes.org/blog_home.asp?display=38|title=UT researchers discover unknown mechanism of membrane fission|website=www.bmes.org|language=en|access-date=2018-09-25}}
13. ^{{cite journal | vauthors = Snead WT, Hayden CC, Gadok AK, Zhao C, Lafer EM, Rangamani P, Stachowiak JC | title = Membrane fission by protein crowding | journal = Proceedings of the National Academy of Sciences of the United States of America | volume = 114 | issue = 16 | pages = E3258–E3267 | date = April 2017 | pmid = 28373566 | pmc = 5402459 | doi = 10.1073/pnas.1616199114 }}

1 : Membrane biology
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/14 10:29:10