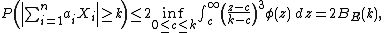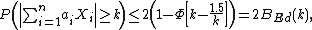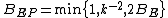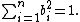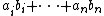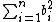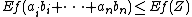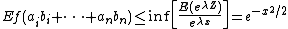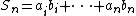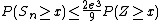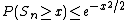“Eaton's inequality”的意思、由来-开放百科全书

In probability theory, Eaton's inequality is a bound on the largest values of a linear combination of bounded random variables. This inequality was described in 1974 by Morris L. Eaton.^[1]

Statement of the inequality

Let {X_i} be a set of real independent random variables, each with an expected value of zero and bounded above by 1 ( |X_i | ≤ 1, for 1 ≤ i ≤ n). The variates do not have to be identically or symmetrically distributed. Let {a_i} be a set of n fixed real numbers with

where φ(x) is the probability density function of the standard normal distribution.

where Φ(x) is cumulative distribution function of the standard normal distribution.

Related inequalities

Let {a_i} be a set of independent Rademacher random variables – P( a_i = 1 ) = P( a_i = −1 ) = 1/2. Let Z be a normally distributed variate with a mean 0 and variance of 1. Let {b_i} be a set of n fixed real numbers such that

This last condition is required by the Riesz–Fischer theorem which states that

for f(x) = | x |^p. The case for p ≥ 3 was proved by Whittle^[4] and p ≥ 2 was proved by Haagerup.^[5]

In the uniform case where all the b_i = n^−1/2 the maximum value of S_n is n^1/2. In this case van Zuijlen has shown that^[9]

References

1. ^Eaton, Morris L. (1974) "A probability inequality for linear combinations of bounded random variables." Annals of Statistics 2(3) 609–614
2. ^Pinelis, I. (1994) "Extremal probabilistic problems and Hotelling's T² test under a symmetry condition." Annals of Statistics 22(1), 357–368
3. ^Dufour, J-M; Hallin, M (1993) "Improved Eaton bounds for linear combinations of bounded random variables, with statistical applications", Journal of the American Statistical Association, 88(243) 1026–1033
4. ^Whittle P (1960) Bounds for the moments of linear and quadratic forms in independent variables. Teor Verojatnost i Primenen 5: 331–335 MR0133849
5. ^Haagerup U (1982) The best constants in the Khinchine inequality. Studia Math 70: 231–283 MR0654838
6. ^Hoeffding W (1963) Probability inequalities for sums of bounded random variables. J Amer Statist Assoc 58: 13–30 MR144363
7. ^Pinelis I (1994) Optimum bounds for the distributions of martingales in Banach spaces. Ann Probab 22(4):1679–1706
8. ^de la Pena, VH, Lai TL, Shao Q (2009) Self normalized processes. Springer-Verlag, New York
9. ^van Zuijlen Martien CA (2011) On a conjecture concerning the sum of independent Rademacher random variables. https://arxiv.org/abs/1112.4988