变换的乘积bianhuan de chengji
是一种变换,相当于连续进行两次变换.在平面或空间的任意两个一一变换F1,F2,对点A先进行第一个变换F1,这时点A变为点A1,即F1(A)→A1;接着进行第二个变换F2,这时,点A1变为点A2,即F2(A1)→A2,这样连续进行F1,F2两个变换,把点A变为点A2的过程,叫做两个变换F1,F2的乘法,记作F2·F1.
能够验证,连续进行两个变换后,结果仍是一个变换,这个变换就是前两个变换的乘积.设变换的乘积为F,前两个变换为F1,F2,则有F=F2·F1.
类似地可以定义有限个变换的乘法和变换的乘积.
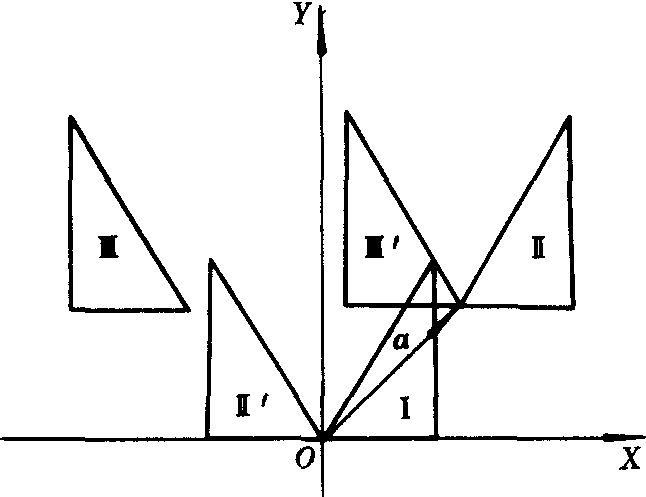
例如,如图,F1是一个沿a的方向和大小移动的平移变换,F2是一个关于Y轴的对称变换,则经过F2·F1,图形Ⅰ变到了图形Ⅱ,又变到了图形Ⅲ.把图形Ⅰ变到图形Ⅲ的变换F,就是F1和F2的乘积,即F=F2·F1.
在一般情况下,变换的乘法不满足交换律,即F2·F1≠F1·F2.如图,先进行变换F2,图形Ⅰ变为图形Ⅱ′,再进行变换F1,把图形Ⅱ′变为图形Ⅲ′,显然F2·F1≠F1·F2.特殊情况下,如两个平移变换的乘积仍是平移变换,而且交换变换的顺序,乘积不变.