回归预测法regression forecast

根据害虫发生与环境因素间的数量关系，用生物统计的回归分析法建立回归方程预测害虫发生的一种方法。适用于害虫中、长期预测预报，并适于利用电子计算机组建方程式和发布预报。一般过程为：选预报因子并测定其和预报量(害虫发生期、发生量、危害程度)的相关显著性；将有显著相关的预报因子和预报量组建回归方程（也称回归式或预测式），并求出回归系数；经可靠性检验修正后，投入实用。
选预报因子 预报因子是对预报量有密切关系的环境因素，须利用多年积累的田间系统调查资料选取。其选择原则是：❶样本数要稍多些，一般10～20个；预报因子数不超过样本数的1/10～1/5;
❷相关性好且稳定；
❸选主要因子和能与之配合或互补的次要因子。其选择方法一般为：❶在直角坐标中作预报因子与预报量的散点图；
❷判断二者的相关性质和程度，经相关系数分析和显著性检验最后选定。
建回归方程 根据预报因子与预报量的关系，回归方程有线性、非线性（曲线）之分，根据预报因子的个数有一元、多元之分。
一元线性回归方程 单一预报因子(x)和预报量(y)呈近似直线关系。建立步骤如下：
求相关系数(γxy)，即求所认定的预报因子与预报量的相关程度。相关系数的公式为：

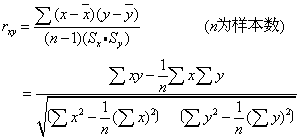
作显著性检验，即检验所选预报因子的相关显著性，常用两法： ❶查相关系数检验表，自由度为n-2，凡公式所求rxy值大于表中0.01的值时，表示相关极显著，大于表中0.05的值时，表示相关显著，则此预报因子可以采用，反之不宜采用；
❷用t检验法。

t=r/Sr=

式中Sr为相关系数标准差。凡t值小于t值表中0.05t值的，不宜选作预报因子。
建立回归方程：

＝a+bx

式中 为预报量估值， a、b为回归系数， 其求算公式为：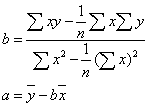

检验预报符合率 （报准次数与预报总次数之比），即检验所建回归方程的符合程度，一般有两种方法：❶回测符合率，即用历史资料代入预测式，统计其符合程度；
❷预测符合率，即用实际发生的资料代入预测式，统计报准百分率。
曲线回归方程 预报因子(x)与预报量(y)成曲线关系时，应建曲线回归方程。建立方法有直接和间接两种：
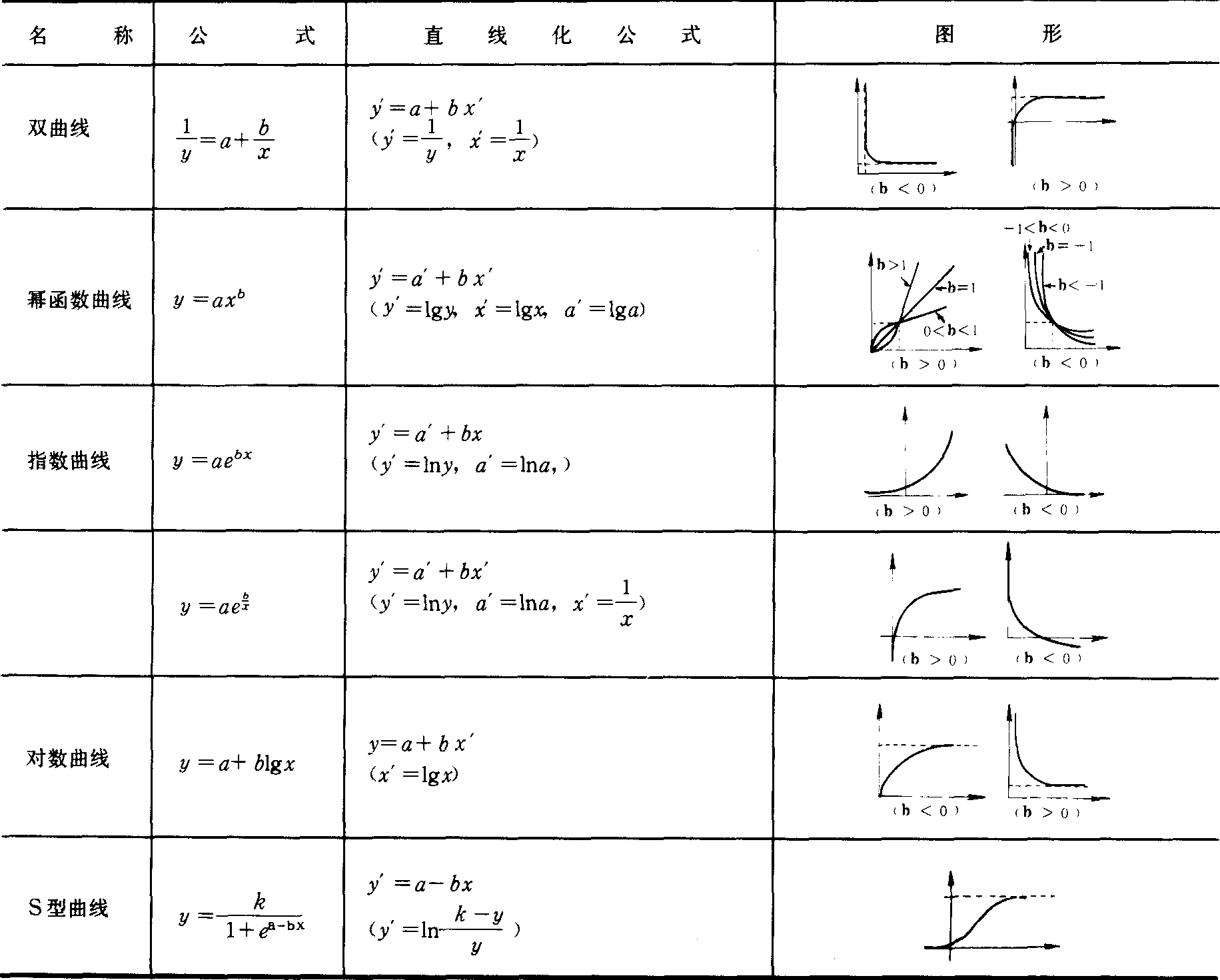
间接法 曲线先化直线，再建立预测式，即首先确定上述曲线可能属于何种常见曲线，再按该常见曲线直线化方法，求出回归方程。常见曲线有双曲线、幂函数曲线、指数曲线、对数曲线、S形曲线、抛物线六种（见表）。

常见曲线表

（续）

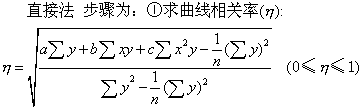
❷计算直线相关系数(γxy)。设ε=η²—γ²，若ε=0，为直线相关，若ε>0，为曲线相关。ε值愈大，曲线相关性愈显著。
❸建立曲线预测式：

＝a+bx+cx²

❹求回归系数a,b,c值：

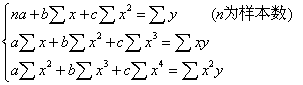
❺用x²表检验所求理论曲线与各实测值的轨迹是否吻合，

式中 y为估计值，y为实际值，查x²表(自由度n—3)，凡所求的x²值大于或等于表中P=0.05的x²值，则所配曲线方程不适合，反之为适合。
多元线性回归方程 当需要采用多个预报因子建立预测式时，可用复相关分析、偏相关分析、逐步回归等法。用复相关法时，可先对预报因子作复相关检验，后建复回归方程，再对此方程用x²表进行适合性检验，和用F检验表作显著性检验。但在实际工作中，因复相关系数难求，常可先建多元回归方程，再对方程进行复相关系数检验或F检验。多元回归方程通式为：

y=b₀+b₁x₁+b₂x₂+……+b_nx_n

式中 b₁,b₂，……，b_n为回归系数，其求法可根据最小二乘法列出方程组：

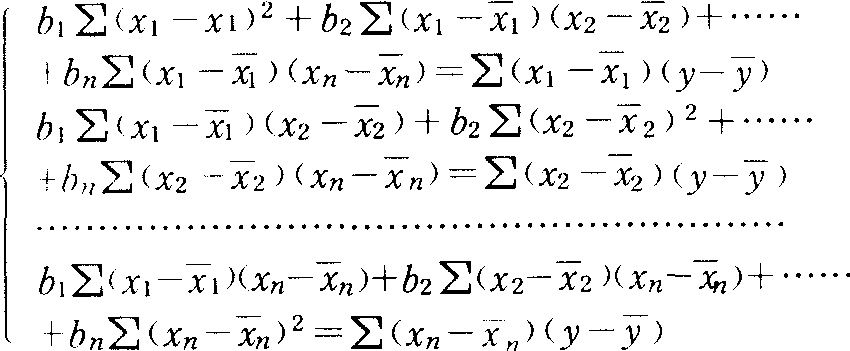
解联立方程组求出b₁,b₂，……，b_n。得

b₀＝ȳ—b1₁—b₂₂……b_n_n

将b₀,b₁,b₂，……bn值代入通式，即得多元线性回归方程。
再对回归方程进行复相关系数检验或F检验。
复相关系数通式为：

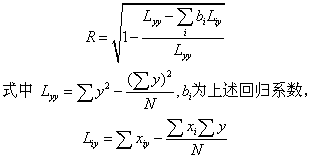
查相关系数显著性表，自由度为(N-K-1)，如算得的R值大于P_0.05的值，则P<0.05，表示相关显著，大于表中P_0.01的值时，则相关极显著。
F检验通式为：

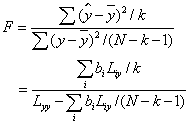
查F表，自由度为(K,N-K-1)，当F值大于F0.05或F_0.01时的F值时，则表示预报量与各因素间相关显著或极显著，回归式成立。