一元方程根的几何意义yiyuan fangcheng gen dejihe yiyi

函数y=f(x)在直角坐标平面上的图象是一条曲线(图1).

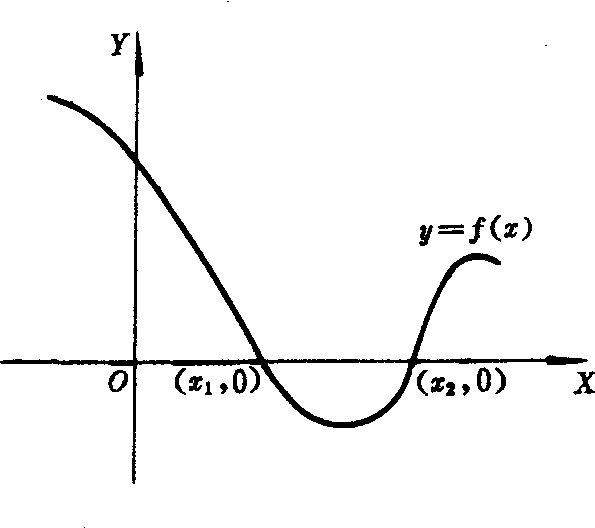
图1

当曲线y=f(x)与x轴相交时，交点的横坐标就是一元方程f(x)=0的实数根.

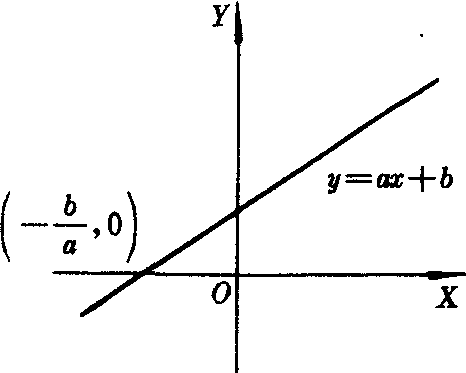
图2

当曲线y=f(x)与x轴没有交点时，一元方程f(x)=0没有实数根.
例如，函数y=ax+b(a≠0)的图象是一条直线(图2).一元一次方程ax+b=0(a≠0)的根x=-b/a就是直线y=ax+b与x轴交点(-b/a,0)的横坐标.
又如，函数y=ax²+bx+c(a≠0)的图象是抛物线.一元二次方程ax²+bx+c=0的根就是抛物线与x轴交点的横坐标.
若判别式△=b²-4ac>0，则方程有两个实数根x₁₂＝(-b±)/2a，此时抛物线y=ax²+bx+c与x轴有两个交点((-b+)/2a,0)

和

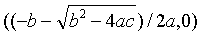
(图3).

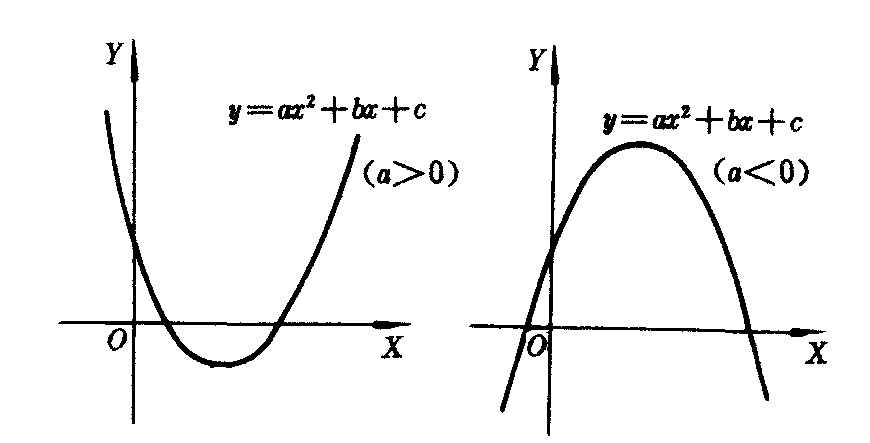
图3

若判别式△_＝b2-4ac=0，则方程有两个实数根x1,₂＝-b/2a，此时抛物线y=ax²+bx+c与x轴相切于顶点(-b/2a,0)(图4).

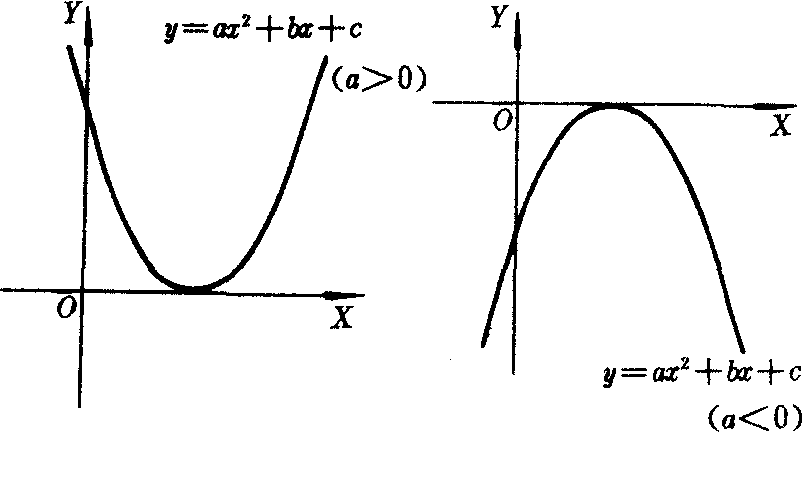
图4

若判别式△=b²-4ac<0，则方程没有实数根，此时抛物线y=ax²+bx+c与x轴没有公共点(图5).

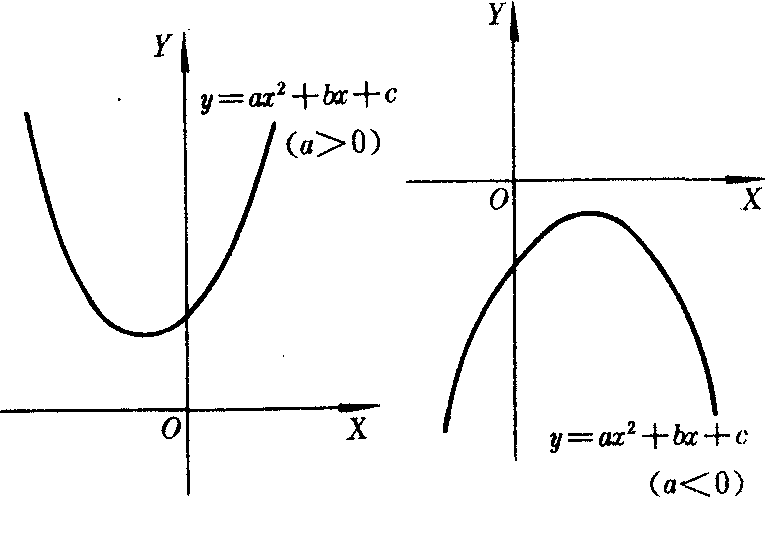
图5