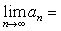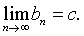实数shishu

有理数和无理数的全体，用R表示.集中每个元素称为一个实数.构造实数集的理论有多种，比较有代表性的主要是戴德金的有理数分割的理论和康托儿的基本系列（或柯西系列）的理论.但不管按哪一种理论所构造的实数集，在同构意义上都是一样的，故实数集可看成唯一确定的.
关于实数集的序关系和加、减、乘、除四则运算，请参阅“戴德金分割”.总之，实数集中四种运算有封闭性，R是个有序数域.
实数域具有连续性，即若对实数域再作分割，则必有x∈R，使A₁中任一元a₁≤x而A₂中任一元a₂≥x，可见实数集中再无“空隙”.
实数集还具有下列性质：
❶阿基米德性：对任二正实数a,b，必有n∈N，使得a
❷有理数和无理数的稠密性：对于任意二实数a,b(a
❸ R的任一个上方有界子集必有上确界；任一个下方有界子集必有下确界；

❹实数的完备性：对于数列{a_n}，若对任意正数ε总能找到一项，从这项以后的任意两项a_m,a_n，恒有|a_m^-a_n|<ε，则{an}称为基本系列，基本系列必有极限.

❺ 区间套原理：两个数列{an},{bn}之间，如果有：a₁≤a₂≤…≤an≤…≤bn≤bn-₁≤…≤b2≤b₁，且(bn-a_n)=0，则必有唯一的c∈R，使得