平面曲线的曲率ping-mian quxian de qulu

设曲线C处处有切线，点M₀为曲线C上的定点，M为曲线上任一点，弧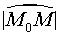的长为s. 给s一个改变量△s，相应地切线有一个转动角Δa，如图1所示.当点M′沿曲线趋向于点M时，若比值Δa/Δs存在极限，则称

为曲线C在点M的曲率.

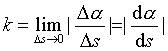
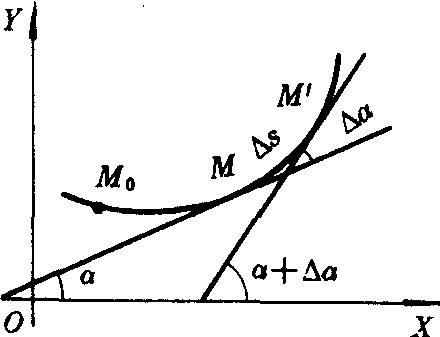
图1

曲线在一点的曲率刻划了光滑曲线在该点处的弯曲程度. 曲率的单位是弧度/单位长.
设函数y=f (x)具有二阶导数，则曲线y=f(x) 在点M (x,y) 的曲率

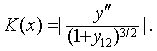
若在曲线C的一点M处，曲率K≠0，则称1/K为曲线C在点M的曲率半径，记作R=1/K.

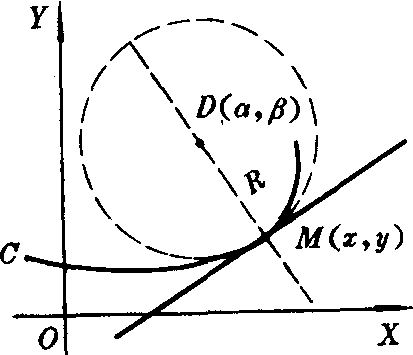
图2

在点M处作曲线C的法线，并在曲线凹的一侧，在法线上取一点D，使|MD|=R，则称以点D为圆心以R为半径的圆为曲线C在点M的曲率圆. 曲率圆的圆心D叫做曲率中心 (图2).曲线C在点M的曲率圆具有以下性质：❶曲率圆与曲线C在点M有公切线.
❷曲率圆和曲线C在点M附近有相同的凸性.
❸曲率圆与曲线C在点M有相同的曲率.
设在曲线y=f (x)上，y″≠ 0，则曲线在点M的曲率中心D (α,β) 的坐标为

曲线在点M的曲率圆的方程为

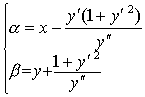
(x-α) ²+ (y-β)²＝R².