归纳guina
从特殊到一般的推理方法.它由推理的前提和结论两部分构成:前提是个别或特殊的判断,结论是从前提中通过推理而获得的,是普遍性判断.
设A={a1,a2,a3,…}是一切可能的特殊情形的集合,对于其中每种情况,某性质C可能为真或为假.假定已知有k个情形性质C成立,即有前提C(a1),C (a2),…,C (ak).那末归纳推理的格式为
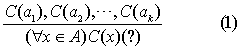
当A为含有K个元素的集合时,前提恰是一切可能的情形,(1)式是等价于
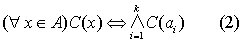
当A包含的元素多于K个或含有无限多个元素时,由于前提没有穷尽一切可能的情形,(1)式中的结论是未必真的,这时按照格式(1)所进行的推理称为不完全归纳法.它不能作为数学证明的方法,然而却是重要的科学发现方法.中学数学教学经常运用此法引出新概念、新法则或作出数学猜想(命题).让学生学会归纳猜想是培养他们创造性的重要途径之一.
归纳Guina
证明方式之一,即用特殊性的论据来证明普遍性的论点的论证方式,就是用一些个别事例推出同一类事物的一般性结论的思维形式。它又分为三种类型:❶完全归纳,即从一类事物中所有对象都具有某种属性而推出这类事物具有这种属性,它适用于包括的对象不多而又可能逐一了解的一类事物。
❷简单枚举,即从一类事物中部分对象具有某种属性而推出这类事物都具有这种属性,它适用于包括对象很多,而又不可能或没必要逐一加以考察的一类事物,但容易犯“轻率概括”或“以偏概全”的错误。
❸科学归纳,即寻求某类事物中部分对象所以具有某种属性的因果关系,然后通过分析推出这类事物都具有这种属性,具体做法又有求同法、求异法等,使用科学归纳,要求对因果关系分析准确,所举出的前提要带有典型性。