拉普拉斯方程Laplace equation
描述在各向同性均质多孔介质(土壤)中饱和水流运动的椭圆型二阶偏微分方程。它表示在三维空间内水势梯度二阶偏导数的总和为零,它有无限个解,求定解时必需满足初始条件和边界条件。当采取直角坐标系统时,该方程可表达如下: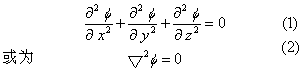 式中:▽为三维向量微分算符,式▽2=0表示水势梯度在三维方向上二阶偏微分。该式的推导:由达西方程一般表达式
式中:▽为三维向量微分算符,式▽2=0表示水势梯度在三维方向上二阶偏微分。该式的推导:由达西方程一般表达式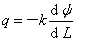 (q为通量,k为饱和导水率,
(q为通量,k为饱和导水率,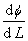 为水势梯度,负号表示水流方向向水势降低方向流动)和连续流方程
为水势梯度,负号表示水流方向向水势降低方向流动)和连续流方程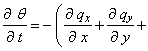
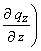 联合得出。将达西方程在三维条件下表达式
联合得出。将达西方程在三维条件下表达式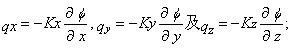 代入连续流方程得出:
代入连续流方程得出: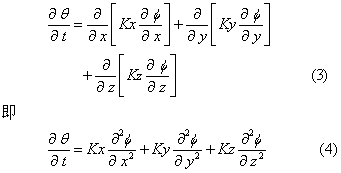
当土壤水分饱和时,所有土壤孔隙为水分充满,土壤含水量θ即为饱和含水量θs,它应与土壤总孔隙度在数值上相等。因此,水流经单元体土壤的出入水量不随时间改变,即
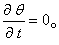 上式也可写成
上式也可写成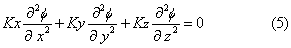 式中:Kx、Ky、Kz代表在三维方向上x、y、z的导水率。当土壤为均一介质条件下,导水率K在各方向上相同,即Kx=Ky=Kz,上式可消去导水率(或饱和导水率各向相同),即可得出拉普拉斯方程。
式中:Kx、Ky、Kz代表在三维方向上x、y、z的导水率。当土壤为均一介质条件下,导水率K在各方向上相同,即Kx=Ky=Kz,上式可消去导水率(或饱和导水率各向相同),即可得出拉普拉斯方程。拉普拉斯方程
形如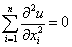 的偏微分方程。更一般的形式为
的偏微分方程。更一般的形式为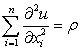 (ρ是已知函数)叫泊松方程。当拉普拉斯方程的解具有连续的二阶偏导数时,称为“调和函数”。在研究重力场,静力场,磁场以及一些物理现象的平衡或稳定过程时,常得到这些方程。
(ρ是已知函数)叫泊松方程。当拉普拉斯方程的解具有连续的二阶偏导数时,称为“调和函数”。在研究重力场,静力场,磁场以及一些物理现象的平衡或稳定过程时,常得到这些方程。
拉普拉斯方程
不存在自由电荷分布的区域中静电场电势所满足的线性微分方程。参见“数学”中的“拉普拉斯方程”。