方差fangeha
设X是一个随机变量,若E [X-E (X)]2存在,则称它为X的方差,记作D (X),即D(X) =E [X-E (X)]2,称 为X的均方差或标准差。
为X的均方差或标准差。
由方差定义知,它是一个非负数,并且可知,若随机变量取值密集在数学期望附近,则方差小;反之则方差大。因此,D (X)是刻划X取值分散程度的一个数字特征。
方差具有以下性质:
❶D (C) =0,C是常数;
❷D (CX) =C2D (X);
❸设X,Y是相互独立随机变量,则
D(X +Y)==D(X)+D(Y),
D(X -Y)= D(X)+D(Y);
❹对于离散型随机变量,则有
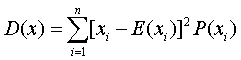
对于连续型随机变量,则有
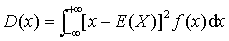
方差fang cha
又称变异数。用S2或V表示。是差异量数之一,代表一组数据的差异情况或离散程度。由各数据与平均数之差即离差自乘之和再除以数据个数而求得。公式为:
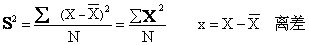
方差
表示随机变量ζ与其数学期望Eζ之间离散程度的一个量。即(ζ-Eζ)2的数学期望。通常记为Dζ或S2,Dζ=Eζ(ζ-Eζ)2。仿此可定义样本的方差S2=1/n (xi-)2,其中为样本x1,x2,…,xn的平均数。这个量也反映了样本的离散程度。
(xi-)2,其中为样本x1,x2,…,xn的平均数。这个量也反映了样本的离散程度。
方差
在总体中指随机变量与其期望的差的期望,用σ2表示。在获得了总体的样本的观察值后,用各观察值与其算术平均值的偏差平方和的算术平均值来估计,记为s2n,即s2n=![]()
![]() (xi-x)2;在n不太大的场合,常用无偏估计s2=
(xi-x)2;在n不太大的场合,常用无偏估计s2=![]()
![]() (xi-x)2去估计σ2,其中n-1是偏差平方和
(xi-x)2去估计σ2,其中n-1是偏差平方和![]() (xi-x)2的自由度。若给出的是已经经过整理的频数分布表,用x1,x2,…,xk表示可能的观察值(或组中值),用fi表示观察到的xi的个数,i=1,2,…,k,又记n=f1+f2+…+fk=
(xi-x)2的自由度。若给出的是已经经过整理的频数分布表,用x1,x2,…,xk表示可能的观察值(或组中值),用fi表示观察到的xi的个数,i=1,2,…,k,又记n=f1+f2+…+fk=![]() fix=
fix=![]()
![]() fixi,则s2=
fixi,则s2=![]()
![]() fi(xi-x)2当x1,x2,…,xk表示组中值时所求得的s2是一个近似值。常被应用于测验分数统计中。
fi(xi-x)2当x1,x2,…,xk表示组中值时所求得的s2是一个近似值。常被应用于测验分数统计中。
方差variance
旧称变异量、变量。离均差的平方和与自由度的比值。常用σ2表示。由样本估计的方差又称均方,常用s2表示。表达式:
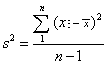
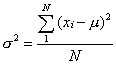
- (二) 控制病虫害,防止粮食霉变
- (二) 推动了创汇农业的发展
- (二) 推动农业现代化、农村工业化和城镇化进程
- (二)推动农村产业结构调整
- (二)推广内容
- (二)推广内容与成效
- (二)推广内容与成果
- (二)推广内容及成果
- (二)推广内容和方法
- (二)推广型煤
- (二) 推广普及农作物优良品种
- (二)推广村民委员会经验
- (二)推广牧草种植
- (二)推广省柴节煤灶
- (二) 推广省柴节煤炉灶
- (二)推广良种
- (二) 推广配、混合饲料
- (二)推广项目及成果
- (二)推行优惠政策,调动农民生产积极性
- (二)推行所长负责制
- (二)推行果业经营形式多元化
- (二)推行目标管理,开展 “创先争优” 活动
- (二) 推行股份合作制
- (二)推进农村工业化、村镇一体化进程
- (二)推进科教兴农