无穷级数wuqiong jishu
将数列 {un} 的项依次用加号连接起来,即
u1 +u2 +…+un +… (1)
或简写为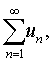 ,称为数项级数或无穷级数。其中u n称为级数 (1)的通项。级数 (1)的前n项和Sn=u1+u2+…+u n称为级数(1)的部分和。若级数(1)的部分和数列{Sn)收敛,设
,称为数项级数或无穷级数。其中u n称为级数 (1)的通项。级数 (1)的前n项和Sn=u1+u2+…+u n称为级数(1)的部分和。若级数(1)的部分和数列{Sn)收敛,设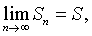 则称级数 (1)收敛,并称S是级数 (1)的和,记作
则称级数 (1)收敛,并称S是级数 (1)的和,记作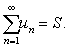 若部分和数列 {Sn) 不存在极限,则称级数 (1)发散。
若部分和数列 {Sn) 不存在极限,则称级数 (1)发散。当级数 (1)收敛于S时,称Rn=S-Sn为级数(1) 的第n个余项,且
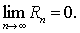
几何级数
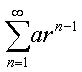 与广义调和级数
与广义调和级数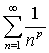 等是最常见的级数。级数
等是最常见的级数。级数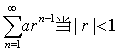 时收敛,其和为
时收敛,其和为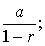 当|r|≥1时发散。级数
当|r|≥1时发散。级数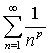 当p>1时收敛;当p≤ 1时发散。
当p>1时收敛;当p≤ 1时发散。无穷级数有如下主要性质:
❶ 若级数
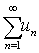 收敛,则
收敛,则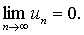
❷ 若级数
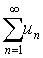 收敛,C为任一常数,则级数
收敛,C为任一常数,则级数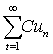 也收敛,且
也收敛,且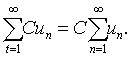
❸若级数
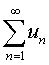 与
与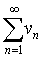 都收敛,则级数
都收敛,则级数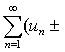 vn) 也收敛,且
vn) 也收敛,且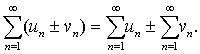
❹ 去掉、增加或改变级数的有限项,并不改变级数的收敛或发散的性质。
❺ 对收敛级数的项任意加括号 (但不改变其次序) 后构成的新级数仍然收敛,且其和不变。
无穷级数理论是数学分析的重要组成部分。无穷级数理论主要用于❶表示函数;
❷近似计算函数值、积分值和微分方程的解。