普遍二次曲面的中心pubian erci qumian de zhonsxin
曲面上任意两点所联的线段叫做弦. 普遍二次曲面一组平行弦的中点的轨迹是一平面. 平分普遍二次曲面的一组平行弦的平面，叫做以该弦的方向为共轭方向的径平面. 普遍二次曲面的所有径平面形成一个平面族. 设普遍二次曲面的方程是F (x,y,z)≡ax2+by2+cz2+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0 (a2+b2+c2+f2+g2+h2≠ 0). 则三个平面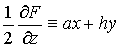
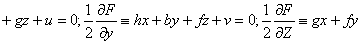+cz+w=0的交点叫做普遍二次曲面的中心. 当中心在曲面上 （即它是奇异点） 时，叫做顶点. 普遍二次曲面不是无轨迹的情况，且方程中一次项的系数都是零，则原点是它的对称中心； 反之，若原点是对称中心，则F (x,y,z) =0所有一次项的系数都是零. 普遍二次曲面不是无轨迹的情况，则中心就是它的对称中心，反过来，对称中心就是它的中心. 设上述三个平面方程构成的方程组的系数矩阵和增广矩阵分别是C及A，即
| 条 件 | 方程组解 的个数 | 中心的情况 | 曲 面 的 形 状 | |
| RC=3 | 唯一解 | 一个中心 | 非顶点 | 椭圆面 （实或虚）、 双曲面 |
| 顶点 | 锥面 （实或虚） | |||
| RC=2 RA=2 | 含一个参 数的解 | 一条直线 的中心 | 非顶点 | 椭圆柱面 （实或虚）、 双曲柱面 |
| 顶点 | 一对相交平面 （实或虚） | |||
| RC=1 RA=1 | 含二个参 数的解 | 一个平面 的中心 | 非顶点 | 一对相异或虚平行平面 |
| 顶点 | 一对重合平面 | |||
| RC=2 RA=3 | 无 解 | 没有中心 | 抛 物 面 | |
| RC=1 RA=2 | 无 解 | 没有中心 | 抛物柱面 | |
| 条 件 | 方程组解 的个数 | 中心的情况 | 曲 面 的 形 状 | |
| RC=3 | 唯一解 | 一个中心 | 非顶点 | 椭圆面 （实或虚）、 双曲面 |
| 顶点 | 锥面 （实或虚） | |||
| RC=2 RA=2 | 含一个参 数的解 | 一条直线 的中心 | 非顶点 | 椭圆柱面 （实或虚）、 双曲柱面 |
| 顶点 | 一对相交平面 （实或虚） | |||
| RC=1 RA=1 | 含二个参 数的解 | 一个平面 的中心 | 非顶点 | 一对相异或虚平行平面 |
| 顶点 | 一对重合平面 | |||
| RC=2 RA=3 | 无 解 | 没有中心 | 抛物面 | |
| RC=1 RA=2 | 无 解 | 没有中心 | 抛物柱面 | |