最短线问题Zuiduanxian wenti
可以看作规划和统筹问题的一种。在平面几何中,两点间的距离以直线为最短。这一原理是许多与几何有关的最短线问题求解的基本思路。
例1: 如图,a是一条公路,现要在a上建一车站c,问站址选在何处可使A、B两村到c的距离之和最短?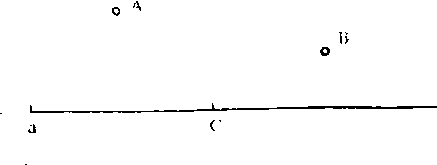
解: 设B关于公路a的对称点为D, 则不论c选在a上何处, 均有c到B、D距离相等。因此,c到A、B距离之和等于c到A、D距离之和,而A到D的距离以直线为最短, 故c的选址应在AD与a的交点处。如图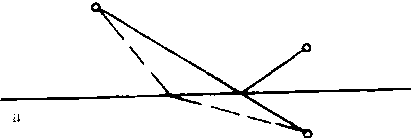
例2: 如图圆柱,AB为底面直径, 求沿侧面由A到C的最短线。
解:把圆柱侧面展开为平面,用直线连接AC,再把平面复原为圆柱面即可。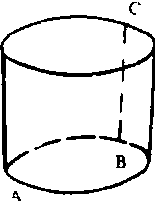
另有一种加权最短路问题, 这类问题不仅要考虑实际距离; 而且须考虑带权的距离。
例3: 设由甲城到乙城有三条道路如图, 且已知每吨公里货物的公路运价是铁路运价的2倍,那么,从甲城到乙城运货选择哪条路线最好?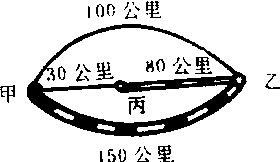
解:考虑到运费,同样数量的货物的公路运价为同样长铁路运价的2倍。这样为公路段赋数2,铁路段赋数1,由甲到乙经由100公里公路的赋数距离为200, 而第二条路线的赋数距离为2×30+80=140,第三条路的赋数距离为150,故以第二条路线为最优。
例4(第二届华罗庚金杯赛复赛):下左面是一张道路图, 每段路上的数字是小王走这段路所需的时间(分)。请问小王从A出发走到B, 最快需要多少时间(分)?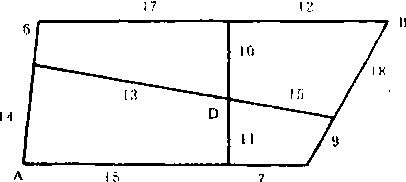
解: 不妨把走各段路所需的时间(分)看作该段路长度。不难看出, 图中的每个四边形中任意三边长度之和大于第四边, 因此可以不考虑绕行某四边形三条边的路径。我们把由A到B的路径分为两类,一类是经过D的,一类是不经过D的,不经过D的路径只有两条,长度都是49分,由A到D的最短路径长为26分,而由D到B的最短路径长为22分。因此小王从A出发走到B, 最快需要48分。