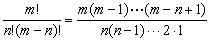组合
在器物造型设计中,把各自独立的不同器物组合在一起,赋予共同的性质和联系,使之能够产生相互配合的关系,这种组合能够达到配套的目的。另外在家具设计中,把不同用途的家俱结合在一起,构成一套完整的大型家俱,称其为组合家俱,更是完全用组合的方法来完成设计的。组合一定要强调相互之间的联系,没有联系则不能称其为组合,只能是拚凑。组合的最终应能够形成一个完整的统一体。
组合zuhe
参见 “排列”。
组合Zuhe
是一种计数问题,提法是: 从有m个元素的集合中, 取出n (n≤m) 个元素 (不计次序),共有多少种不同取法?取法总数称为从m个元素中取n个元素的组合数,记为Cmn。考虑到n个元素共有n! (n的全排列) 种不同顺序, 故Cmn=Amn/n!=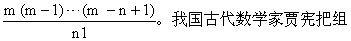
合数排成下面的三角形,称为贾宪三角(参见“贾宪”条)。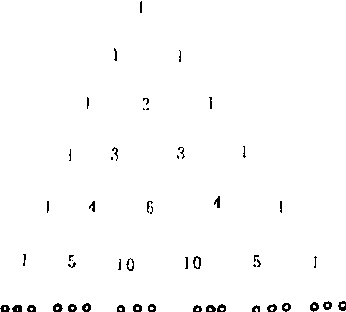
这一三角形的构作方法为:边上的数都是1,中间的数依从上到下的顺序逐行计算, 法则是每个数等于它肩头两个数的和。这个三角形中第m+1行的第n+1个数恰为Cnm。从贾宪三角中可以发现组合数的一些有趣性质如:
Cnm=Cn-1m-1+Cnm-1 (n≤m-1),
C0m+Cm1+…+Cmm=2m, 以及Cmn=Cmm-n等。
例1: 下图中共有多少个矩形?
解: 这样的问题用直接数的办法当然是不足取的。图中的每个矩形可由它的左、右,上、下两组对
边唯一确定, 而水平的线段有4条, 铅直的线段有5条, 故矩形个数为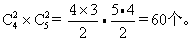
例2: 如图, 由A到B不同的最短路线共有多少条?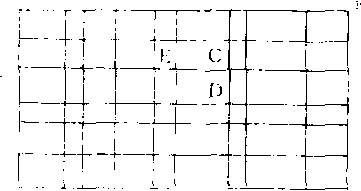
解: 设C为图中任何一个交叉点,则由A出发到C的任意一条最短路径或是经过C的左邻E点,或是经过C的下邻D点,那么由A到C的最短路径数目等于由A到D及由A到E的最短路径数目之和,而A到图的左边或下边任何一点都只有唯一的最短路径, 这使我们想到贾宪三角、A到B的最短路径数目为
C10+7-21(7-1)=C156=5 005。
这一问题也可以考虑如下:由A到B的最短路线总共要走15段街,而其中9段是由西向东(沿图中的水平方向走),6段是由南向北(沿图中的铅直方向走),得到同样的结果。
例3:把9本同样的书放在三个不同的抽屉里,每个抽屉至少放一本, 共有多少种不同的放法?
解:我们考虑从1—8八个自然数中选出两个的组
抽屉中放的书册数及第一、二两个抽屉中放书册数之和是介于1与8之间的两个不同的自然数, 任何一种放法由这两个数唯一确定。因此, 放法总数为28。
此外, 也可以讨论有重复元素的组合问题。
例4:有红、黄、蓝色的球各10个, 从中选取15个球, 共有多少种不同结果?
解:先考虑一种简单的情况:各种颜色的球都不少于15个,设r、y分别表示取出的15个球中红球与黄球的个数, 那么一种选取结果可由两个不相等的数r与r+y+1唯一决定,而这两个数大于等于0,小于等
再来看上述136种可能当中, 某种颜色的球多于10个的不同结果有多少?不妨设红球多于10个,问题转变为:事先已取出11个红球,其余4个球从三种颜色的球当中取,有多少不同结果?与前面的讨论类似,可得在先取11个红球的前提下, 不同结果的数目是C26=15。
原题的答案应为 136-3×15=91种。这里136为对各种球的数目不加任何限制的结果数, 而3×15为某种颜色的球多于10个的不同结果数目,二者之差为每种颜色的球均不超过10个的不同结果数目。
组合Zuhe
在工艺美术设计中,把各自独立的、不同的构成部分组织在一起,赋予共同的性质而产生联系,使之能够产生相互配合的关系,这种组织和配合能够达到配套的目的,更有利于使用要求,或是更加强表现力。组合一定要强调联系,相互之间没有联系则不容易获得整体效果,只能是简单的拼凑。组合的最终目的是能够出现一个新的、完整的统一体。例如:组合家具的设计,就是把不同使用要求的家具结合在一起,构成一套具有多方面使用要求的家具。在造型风格和工艺材料及色彩质地诸方面,又是一致的,既统一,又有变化。餐具配套也是一种组合,是各种盘、碗、杯、碟、壶等造型的组合。
组合
从m个不同元素中取出n(n≤m)个不同的元素成为一组,称为一个组合。所有这样得到的不同组合的数目是