二次曲线的不变量erci quxian de bubianliang
如果二次曲线的方程Ax2+Bxy+Cy2+Dx+Ey+F=0经过任意坐标变换后得到一个新方程A'x2+B'xy+C'y2+D'x+E'y+F'=0,由系数A,B,C,D,E,F所组成的一个函数f,若和由对应系数A′,B′,C′,D′,E′,F′所组成的相同的这个函数的值总是相等,即在不同的直角坐标系下总有f(A,B,C,D,E,F)=f(A′,B′,C′,D′,E′,F′),那么称这个函数f为方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示的二次曲线在直角坐标系下坐标变换的不变量.
定理 二次曲线Ax2+Bxy+Cy2+Dx+Ey+F=0在移轴和转轴变换下的不变量是H,△和I.其中 H=A+C=A′+C′
△=B2-4AC= B′2-4A′C′
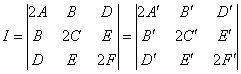
利用不变量可以检验移轴、转轴过程中,可能发生的计算错误,有时还可以用它们来简化转轴运算。用不变量来刻划曲线的几何特性,这在理论上有普遍意义.