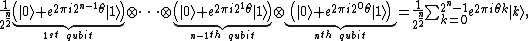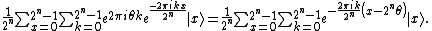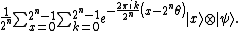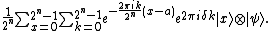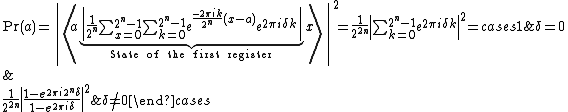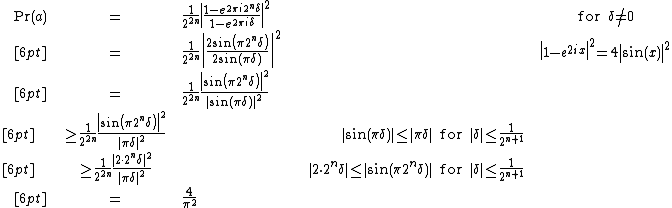“Quantum phase estimation algorithm”的意思、由来-开放百科全书

词条

Quantum phase estimation algorithm

释义

The problem
The algorithm
Setup Create superposition Apply controlled unitary operations Apply inverse Quantum Fourier transform Phase approximation representation Measurement
See also
References

{{Use American English|date=January 2019}}{{Short description|Quantum algorithm for eigenvalue estimation
}}

The Quantum phase estimation algorithm (also referred to as quantum eigenvalue estimation algorithm), is a quantum algorithm to estimate the phase (or eigenvalue) of an eigenvector of a unitary operator. More precisely, given a unitary matrix and a quantum state such that 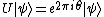, the algorithm estimates the value of with high probability within additive error , using 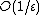controlled-U operations.

Phase estimation is frequently used as a subroutine in other quantum algorithms, such as Shor's algorithm^[1]{{rp|131}} and the quantum algorithm for linear systems of equations.

The problem

Let U be a unitary operator that operates on m qubits with an eigenvector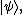 such that .

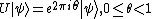We would like to find the eigenvalue 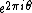of , which in this case is equivalent to estimating the phase , to a finite level of precision. We can write the eigenvalue in the form 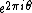because U is a unitary operator over a complex vector space, so its eigenvalues must be complex numbers with absolute value 1.

The algorithm

Setup

The input consists of two registers (namely, two parts): the upper qubits comprise the first register, and the lower qubits are the second register.

Create superposition

The initial state of the system is 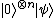. After applying n-bit Hadamard gate operation 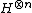on the first register, the state of the first register can be described as

.

Apply controlled unitary operations

Let be a unitary operator with eigenvector such that 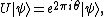thus

.

is a controlled-U gate which applies the unitary operator on the second register only if its corresponding control bit (from the first register) is .

After applying all the controlled operations 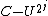with as seen in the figure, and using 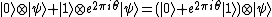, the state of the first register can be described as

where denotes the binary representation of .

Apply inverse Quantum Fourier transform

Applying inverse Quantum Fourier transform on

yields

The state of both registers together is

Phase approximation representation

We can approximate the value of 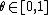by rounding 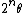to the nearest integer. This means that 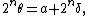where is the nearest integer to 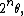and the difference 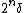satisfies .

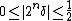We can now write the state of the first and second register in the following way:

Measurement

Performing a measurement in the computational basis on the first register yields the result with probability

For the approximation is precise, thus 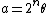and 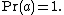In this case, we always measure the accurate value of the phase.^[2]{{rp|157}}^[3]{{rp|347}} The state of the system after the measurement is 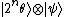.^[1]{{rp|223}}

For 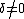since 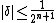the algorithm yields the correct result with probability 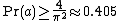. We prove this as follows: ^[2]{{rp|157}} ^[3]{{rp|348}}

This result shows that we will measure the best n-bit estimate of with high probability. By increasing the number of qubits by 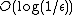and ignoring those last qubits we can increase the probability to .^[3]

References

1. ^¹{{cite book|last1=Chuang|first1=Michael A. Nielsen & Isaac L.|title=Quantum computation and quantum information|date=2001|publisher=Cambridge Univ. Press|location=Cambridge [u.a.]|isbn=978-0521635035|edition=Repr.}}
2. ^¹{{cite book|last1=Benenti|first1=Guiliano|last2=Casati|first2=Giulio|last3=Strini|first3=Giuliano|title=Principles of quantum computation and information|date=2004|publisher=World Scientific| location=New Jersey [u.a.]|isbn=978-9812388582|edition=Reprinted.}}
3. ^¹²{{cite journal| last1=Cleve| first1=R.| last2=Ekert |first2=A. |last3=Macchiavello| first3=C.| last4=Mosca|first4=M.|title=Quantum algorithms revisited|journal=Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences|date=8 January 1998| volume=454| issue=1969|doi=10.1098/rspa.1998.0164|arxiv=quant-ph/9708016|bibcode=1998RSPSA.454..339C}}

{{cite arXiv | eprint=quant-ph/9511026| last1= Kitaev| first1= A. Yu.| title= Quantum measurements and the Abelian Stabilizer Problem| year= 1995}}

1 : Quantum algorithms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。