三个向量共面的充要条件sange xiangliang gongmian dechongyao tiaojian

定理1 三个向量a,b,c共面的充要条件是存在不全为零的m,n,l，使ma+nb+lc=0成立.
推论1.1 a,b不共线，c与a,b共面的充要条件是存在由a,b,c唯一确定的α,β，使得c=αa+βb成立.
推论1.2 a,b,c不共面，则ma+nb+lc=0的充要条件是m=n=l=0.
以上定理和推论可改用空间四点的位置向量表述，相应地有：
定理2 空间四点A,B,C,D共面的充要条件是存在不全为零的m,n,l,s，满足m+n+l+s=0且使mA+nB+lC+sD=0成立.
推论2.1 若三点A,B,C不共线，则点D与A,B,C共面的充要条件是D=mA+nB+lC.其中m,n,l不全为零，且m+n+l=1.
推论2.2 若空间四点A,B,C,D不共面，则等式mA+nB+lC+sD=0成立且m+n+l+s=0的充分必要条件是m=n=l=s=0.
假如我们讨论的向量任意两个都不共线，以上两个定理四个推论大都具有更为明确的表述.
定理1′ 三个向量a,b,c中任两个向量不共线，则它们共面的充要条件是存在全不为零的m,n,l，使ma+nb+lc=0成立.
推论1.1′ 向量a,b,c共面且无两个向量共线的充分必要条件是存在由a,b,c唯一确定的全不为零的α,β，使c=αa+βb.
推论1.2′ 与推论1.2相同.
定理2′ 空间四点A,B,C,D中无三点共线，则它们共面的充要条件是存在全不为零的m,n,l,s，满足m+n+l+s=0且使mA+nB+lC+sD=0成立.
推论2.1′ 无三点共线的四点A,B,C,D共面的充要条件是存在全不为零的m,n,l，满足m+n+l=1且使D=mA+nB+lC成立.
推论2.2′ 与推论2.2相同.

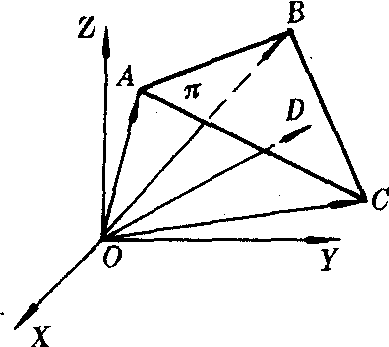
图1

推论2.1相当于以和为基向量建立了一个三维仿射坐标基底(见图1).由不共线三点A,B,C所确定的平面π是这个坐标基底的单位平面.任一个以O为起点的向量都可用A,B,C线性表出，如D=mA+nB+lC.(m,n,l)就是D在此坐标基底下的坐标.当D点在单位平面π上时，其三个坐标分量m,n,l之和等于1.当D点在单位平面π之外O点同侧时，m+n+l<1.当D点在单位平面π之外O点异侧时，m+n+l>1.反之也成立.也就是说，上面所总结的D点的位置与其三个坐标分量之和之间的关系是充分必要的.这个单位平面π相当于平面仿射坐标系或平面直角坐标系中过(1,0)和(0,1)点的直线(如图2、图3).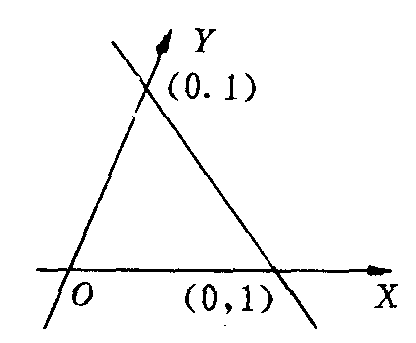

图2

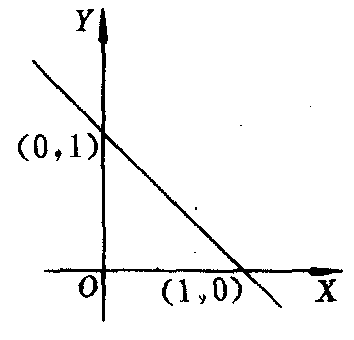
图3

前面总结的结论是我们已在二维空间中得到的结论在三维空间中的推广.