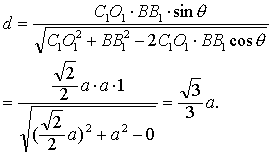异面直线距离的一种计算公式yimian zhixian juli deyizhong jisuan gongshi

如图1，设l,m为两条异面直线.过m作两个平面α,β分别交l于A,B.点A到m的距离AC=a，点B到m的距离BD=b.二面角α-m-β为θ.则异面直线l,m的距离为

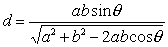
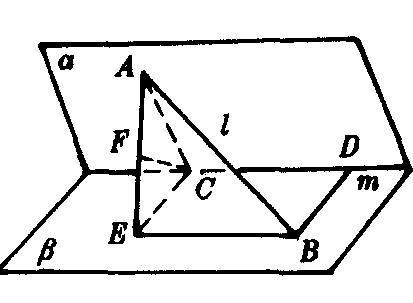
图1

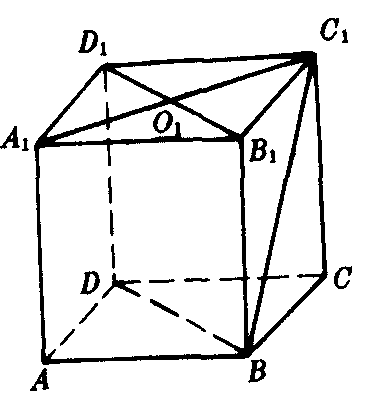
图2

证 在平面β内过C作CE⊥CD，过B作CD的平行线与CE交于E，则∠ACE=θ,CE=b，连结AE.容易证明平面ACE⊥平面AEB.在平面ACE中，作CF⊥AE于F，则CF⊥平面AEB，即CF是C点到平面AEB的距离.因为CD∥平面AEB，所以CF是CD到平面AEB的距离，也就是l到m的距离.
在△ACE中，因为

AC·CE·sinθ = CF·AE

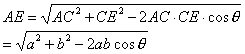
所以

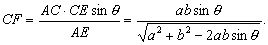
例 如图2，正方体ABCD-A₁B₁C₁D₁的棱长为a.求B₁D₁与BC₁间的距离.
解 作对角面BD₁，则B₁D₁是平面BD₁与平面B₁C₁D₁的交线，连结A₁C₁.设A₁C₁∩B₁D₁＝O₁，则C₁O₁

⊥B1D1

即C1到B1D1的距离为

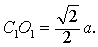
而B到

B₁D₁的距离为BB₁＝a.又平面B₁C₁D₁与对角面BD₁垂直，因此θ=90°.代入上述公式，得