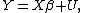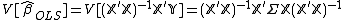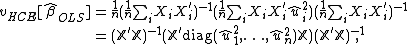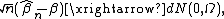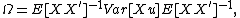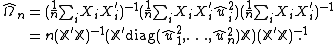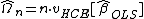1. Definition

2. Eicker's heteroscedasticity-consistent estimator

3. See also

4. Software

5. References

6. Further reading

The topic of heteroscedasticity-consistent (HC) standard errors arises in statistics and econometrics in the context of linear regression as well as time series analysis. These are also known as Eicker–Huber–White standard errors (also Huber–White standard errors or White standard errors),^[1] to recognize the contributions of Friedhelm Eicker,^[2] Peter J. Huber,^[3] and Halbert White.^[4]

In regression and time-series modelling, basic forms of models make use of the assumption that the errors or disturbances u_i have the same variance across all observation points. When this is not the case, the errors are said to be heteroscedastic, or to have heteroscedasticity, and this behaviour will be reflected in the residuals estimated from a fitted model. Heteroscedasticity-consistent standard errors are used to allow the fitting of a model that does contain heteroscedastic residuals. The first such approach was proposed by Huber (1967), and further improved procedures have been produced since for cross-sectional data, time-series data and GARCH estimation.

Definition

Assume that we are studying the linear regression model

where X is the vector of explanatory variables and β is a k × 1 column vector of parameters to be estimated.

The ordinary least squares (OLS) estimator is

where 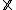denotes the matrix of stacked 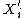values observed in the data.

If the sample errors have equal variance σ² and are uncorrelated, then the least-squares estimate of β is BLUE (best linear unbiased estimator), and its variance is easily estimated with

where 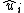are regression residuals.

When the assumptions of 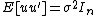are violated, the OLS estimator loses its desirable properties. Indeed,

where .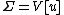

While the OLS point estimator remains unbiased, it is not "best" in the sense of having minimum mean square error, and the OLS variance estimator does not provide a consistent estimate of the variance of the OLS estimates.

For any non-linear model (for instance Logit and Probit models), however, heteroscedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroscedasticity).^[5][6] As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption.”^[7]

Eicker's heteroscedasticity-consistent estimator

If the regression errors are independent, but have distinct variances σ_i², then 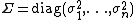which can be estimated with 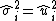. This provides White's (1980) estimator, often referred to as HCE (heteroscedasticity-consistent estimator):

where as above 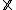denotes the matrix of stacked 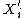values from the data. The estimator can be derived in terms of the generalized method of moments (GMM).

Note that also often discussed in the literature (including in White's paper itself) is the covariance matrix 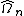of the -consistent limiting distribution:

where,

and

Thus,

and

.

Precisely which covariance matrix is of concern should be a matter of context.

Alternative estimators have been proposed in MacKinnon & White (1985) that correct for unequal variances of regression residuals due to different leverage.^[8] Unlike the asymptotic White's estimator, their estimators are unbiased when the data are homoscedastic.

See also

• Generalized least squares
• Generalized estimating equations
• Weighted least squares
• White test — a test for whether heteroscedasticity is present.
• Newey–West estimator

Software

• EViews: EViews version 8 offers three different methods for robust least squares: M-estimation (Huber, 1973), S-estimation (Rousseeuw and Yohai, 1984), and MM-estimation (Yohai 1987).^[9]
• MATLAB: See the hac function in the Econometrics toolbox.^[10]
• Python: The Statsmodel package offers various robust standard error estimates, see statsmodels.regression.linear_model.RegressionResults for further descriptions
• R: the sandwich package via the vcovHC() command.^[11][12]
• RATS: robusterrors option is available in many of the regression and optimization commands (linreg, nlls, etc.).
• Stata: robust option applicable in many pseudo-likelihood based procedures.^[13]
• Gretl: the option --robust to several estimation commands (such as ols) in the context of a cross-sectional dataset produces robust standard errors.^[14]

References

Further reading

• {{Cite journal |last=Hayes |first=Andrew F. |last2=Cai |first2=Li |title=Using heteroscedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation |journal=Behavior Research Methods |volume=39 |issue=4 |pages=709–722 |doi=10.3758/BF03192961 |year=2007 }}
• {{cite journal |first=Gary |last=King |authorlink=Gary King (political scientist) |first2=Margaret E. |last2=Roberts |title=How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It |journal=Political Analysis |volume=23 |issue=2 |year=2015 |pages=159–179 |doi=10.1093/pan/mpu015 }}
• {{Cite book |last=Wooldridge |first=Jeffrey M. |authorlink=Jeffrey Wooldridge |chapter=Heteroskedasticity-Robust Inference after OLS Estimation |title=Introductory Econometrics : A Modern Approach |edition=Fourth |location=Mason |publisher=South-Western |year=2009 |isbn=978-0-324-66054-8 |pages=265–271 }}

• German submarine U-547
• German submarine U-548
• German submarine U-560
• German submarine U-561
• German submarine U-562
• German submarine U-563
• German submarine U-565
• German submarine U-567
• German submarine U-568
• German submarine U-569
• German submarine U-572
• German submarine U-574
• German submarine U-575
• German submarine U-576
• German submarine U-577
• German submarine U-578
• German submarine U-579
• German submarine U-580
• German submarine U-581
• German submarine U-58 (1938)
• German submarine U-58 (1939)
• German submarine U-582
• German submarine U-583
• German submarine U-584
• German submarine U-585