求积问题Qiujiwenti
包括求平面图形面积以及求空间中物体的体积等。求积的基本公式和基本方法包括:❶长方形面积等于长乘宽,长方体体积等于长乘宽乘高。
❷圆面积等于圆周率乘半径平方。
❸挖补,从一平面图形(空间物体)上挖掉一块,补在同一图形其他部位,图形(物体)的面积(体积)不变。据此方法,可求得平行四边形面积。
❹对称图形(物体)面积(体积)相等,据此,可得三角形,梯形的求积公式。
❺比例方法, 相似图形面积之比等于对应线段长度之比的平方。
例1 (第一届华罗庚金杯赛复赛): 一个长方形(如右图),被两条直线分成四个长方形,其中三个的面积分别是20公亩、25公亩和30公亩, 问另一个 (图中的阴影部分) 长方形的面积是多少公亩?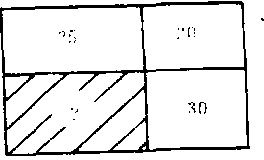
解:设S1代表阴影部分长方形面积,S2=30, S3=20, S4=25(公亩)分别代表其余三个长方形的面积,那么S1:S2=S4:S3,这是因为长方形面积等于长乘宽, 如果有两个矩形的一对边相等,那么它们的面积之比等于另一对边长度之比。因此S1=25×30/20=37.5(公亩)。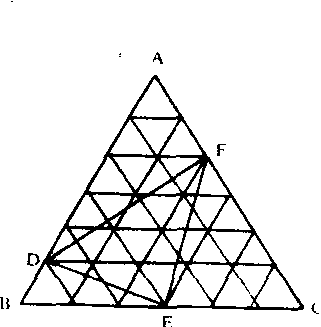
例2: 已知三角形ABC(如右图)中每个小等边三角形的面积是1平方厘米, 求三角形DEF的面积。
解: 在BC边外取G点(如图), 简单地数小三角形可知平行四边形ADGF的面积为20平方厘米, 而三角形ADF的面积是此平行四边形面积的一半, 故三角形ADF的面积为10平方厘米, 同理可知三角形BED与ECF的面积分别是3和12平方厘米, 而三角形ABC的面积是36平方厘米,减去三个三角形面积,得到三角形DEF的面积为11平方厘米。
例3: 任何直角三角形斜边的平方等于两直角边的平方和。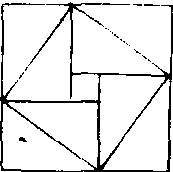
不妨设直角三角形两直角边为a、b,斜边为c,作边长为c的正方形,由此正方形各边向内作直角边长度为a、b的直角三角形。各三角形面积均为1/2ab,而里面的小正方形面积为(a-b)2,于是大正方形面积等于2ab+(a-b)2=a2+b2, 另一方面大正方形面积等于c2,故c2=a2+b2。这一结论称为勾股定理。
例4:右图的长方形长和宽分别为a、b,以四条边和一条对角线为直径作圆, 求图中阴影部分的面积。
解: 整个图形面积等于长方形与四个半圆面积之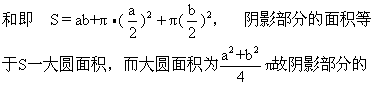
面积是ab,就是说阴影部分的面积与长方形的面积相等。