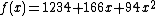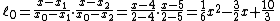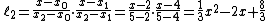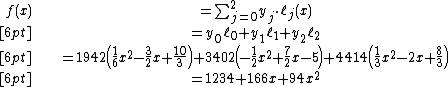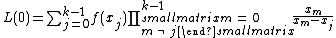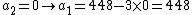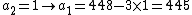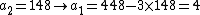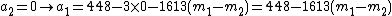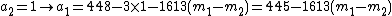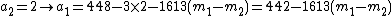- High-level explanation
- Mathematical definition
- Shamir's secret-sharing scheme
- Usage Example Preparation Reconstruction Computationally efficient approach Problem Solution Python example
- Properties
- See also
- References
}}
Shamir's Secret Sharing is an algorithm in cryptography created by Adi Shamir. It is a form of secret sharing, where a secret is divided into parts, giving each participant its own unique part.
To reconstruct the original secret, a minimum number of parts is required. In the threshold scheme this number is less than the total number of parts. Otherwise all participants are needed to reconstruct the original secret.
High-level explanation
Shamir's Secret Sharing is used to secure a secret in a distributed way, most often to secure other encryption keys. The secret is split into multiple parts, called shares. These shares are used to reconstruct the original secret.
To unlock the secret via Shamir's secret sharing, you need a minimum amount of shares. This is called the threshold, and is used to denote the minimum amount of shares needed to unlock the secret. Let us walk through an example:
Problem: Company XYZ needs to secure their vault's passcode. They could use something standard, such as AES, but what if the holder of the key passes away? What if the key is compromised via a malicious hacker? Or, what if the holder of the key turns rogue, and uses his power over the vault to his benefit?This is where SSS comes in. It can be used to encrypt the vault's passcode, and generate a certain amount of shares, where a certain amount of shares can be allocated to each executive within Company XYZ. Now, only if they pool their shares together can they unlock the vault. The threshold can be appropriately set for the number of executives, so the vault is always able to be accessed by the authorized individuals. Should a share or two fall into the wrong hands, they couldn't open the passcode unless they had cooperation from the other executives.
Mathematical definition
The goal is to divide secret  (for example, the combination to a safe) into
(for example, the combination to a safe) into  pieces of data
pieces of data  in such a way that:
in such a way that:
- Knowledge of any
 or more
or more  pieces makes
pieces makes  easy to compute. That is, the complete secret
easy to compute. That is, the complete secret  can be reconstructed from any combination of
can be reconstructed from any combination of  pieces of data.
pieces of data. - Knowledge of any
 or fewer
or fewer  pieces leaves
pieces leaves  completely undetermined, in the sense that the possible values for
completely undetermined, in the sense that the possible values for  seem as likely as with knowledge of
seem as likely as with knowledge of  pieces. Said another way, the secret
pieces. Said another way, the secret  cannot be reconstructed with fewer than
cannot be reconstructed with fewer than  pieces.
pieces.
This scheme is called  threshold scheme.
threshold scheme.
If  then every piece of the original secret
then every piece of the original secret  is required to reconstruct the secret.
is required to reconstruct the secret.
Shamir's secret-sharing scheme
The essential idea of Adi Shamir's threshold scheme is that 2 points are sufficient to define a line, 3 points are sufficient to define a parabola, 4 points to define a cubic curve and so forth.
That is, it takes 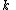 points to define a polynomial of degree
points to define a polynomial of degree  .
.
Suppose we want to use a  threshold scheme to share our secret
threshold scheme to share our secret  , without loss of generality assumed to be an element in a finite field
, without loss of generality assumed to be an element in a finite field  of size
of size  where
where 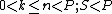 and
and  is a prime number.
is a prime number.
Choose at random  positive integers
positive integers 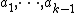 with
with 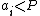 , and let
, and let 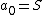 . Build the polynomial
. Build the polynomial  . Let us construct any
. Let us construct any 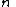 points out of it, for instance set
points out of it, for instance set 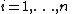 to retrieve
to retrieve 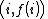 . Every participant is given a point (a non-zero integer input to the polynomial, and the corresponding integer output) along with the prime which defines the finite field to use.
. Every participant is given a point (a non-zero integer input to the polynomial, and the corresponding integer output) along with the prime which defines the finite field to use.
Given any subset of 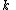 of these pairs, we can find the coefficients of the polynomial using interpolation. The secret is the constant term
of these pairs, we can find the coefficients of the polynomial using interpolation. The secret is the constant term 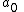 .
.
Usage
Example
The following example illustrates the basic idea. Note, however, that calculations in the example are done using integer arithmetic rather than using finite field arithmetic. Therefore the example below does not provide perfect secrecy and is not a true example of Shamir's scheme. So we'll explain this problem and show the right way to implement it (using finite field arithmetic).
Preparation
Suppose that our secret is 1234  .
.
We wish to divide the secret into 6 parts 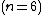 , where any subset of 3 parts
, where any subset of 3 parts 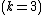 is sufficient to reconstruct the secret. At random we obtain
is sufficient to reconstruct the secret. At random we obtain  numbers: 166 and 94.
numbers: 166 and 94.
where
is secret
Our polynomial to produce secret shares (points) is therefore:
We construct six points 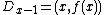 from the polynomial:
from the polynomial:
We give each participant a different single point (both 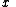 and
and 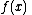 ). Because we use
). Because we use 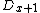 instead of
instead of  the points start from
the points start from  and not
and not  . This is necessary because
. This is necessary because  is the secret.
is the secret.
Reconstruction
In order to reconstruct the secret any 3 points will be enough.
Let us consider  .
.
We will compute Lagrange basis polynomials:
Therefore
Recall that the secret is the free coefficient, which means that  , and we are done.
, and we are done.
Computationally efficient approach
Considering that the goal of using polynomial interpolation is to find a constant in a source polynomial  using Lagrange polynomials "as it is" is not efficient, since unused constants are calculated.
using Lagrange polynomials "as it is" is not efficient, since unused constants are calculated.
An optimized approach to use Lagrange polynomials to find 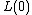 is defined as follows:
is defined as follows:
Problem
Although the simplified version of the method demonstrated above, which uses integer arithmetic rather than finite field arithmetic, works fine, there is a security problem: Eve gains a lot of information about  with every
with every  that she finds.
that she finds.
Suppose that she finds the 2 points 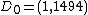 and
and 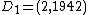 ,
,
she still doesn't have  points so in theory she shouldn't have gained any more info about
points so in theory she shouldn't have gained any more info about  .
.
But she combines the info from the 2 points with the public info:  and she :
and she :
|fills the
 -formula with
-formula with  and the value of
and the value of 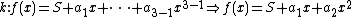
|fills (i) with the values of
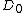 's
's  and
and 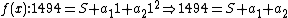
|fills (i) with the values of
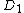 's
's  and
and 
|does (iii)-(ii):
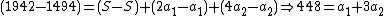 and rewrites this as
and rewrites this as 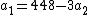
|knows that
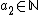 so she starts replacing
so she starts replacing  in (iv) with 0, 1, 2, 3, ... to find all possible values for
in (iv) with 0, 1, 2, 3, ... to find all possible values for 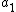 :
:After  she stops because she reasons that if she continues she would get negative values for
she stops because she reasons that if she continues she would get negative values for 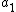 (which is impossible because
(which is impossible because 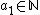 ), she can now conclude
), she can now conclude 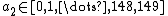
|replaces
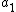 by (iv) in (ii):
by (iv) in (ii): 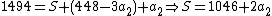
|replaces in (vi)
 by the values found in (v) so she gets
by the values found in (v) so she gets  which leads her to the information:
which leads her to the information:}}
She now only has 150 numbers to guess from instead of an infinite number of natural numbers.
Solution
Geometrically this attack exploits the fact that we know the order of the polynomial and so gain insight into the paths it may take between known points this reduces possible values of unknown points since it must lie on a smooth curve.
This problem can be fixed by using finite field arithmetic. A field of size  is used. The graph shows a polynomial curve over a finite field, in contrast to the usual smooth curve it appears very disorganised and disjointed.
is used. The graph shows a polynomial curve over a finite field, in contrast to the usual smooth curve it appears very disorganised and disjointed.
In practice this is only a small change, it just means that we should choose a prime  that is bigger than the number of participants and every
that is bigger than the number of participants and every  (including
(including 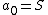 ) and we have to calculate the points as
) and we have to calculate the points as 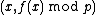 instead of
instead of 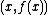 .
.
Since everyone who receives a point also has to know the value of  , it may be considered to be publicly known. Therefore, one should select a value for
, it may be considered to be publicly known. Therefore, one should select a value for  that is not too low.
that is not too low.
Low values of  are risky because Eve knows
are risky because Eve knows 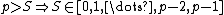 , so the lower one sets
, so the lower one sets  , the fewer possible values Eve has to guess from to get
, the fewer possible values Eve has to guess from to get  .
.
For this example we choose 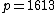 , so our polynomial becomes
, so our polynomial becomes  which gives the points:
which gives the points: 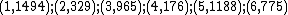
This time Eve doesn't win any info when she finds a  (until she has
(until she has  points).
points).
Suppose again that Eve finds  and
and 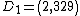 , this time the public info is:
, this time the public info is:  so she:
so she:
|fills the
 -formula with
-formula with  and the value of
and the value of  and
and  :
: 
|fills (i) with the values of
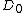 's
's  and
and 
|fills (i) with the values of
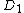 's
's  and
and 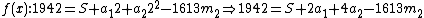
|does (iii)-(ii):
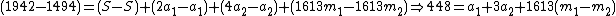 and rewrites this as
and rewrites this as 
|knows that
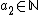 so she starts replacing
so she starts replacing  in (iv) with 0, 1, 2, 3, ... to find all possible values for
in (iv) with 0, 1, 2, 3, ... to find all possible values for 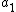 :
:}}
This time she can't stop because 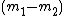 could be any integer (even negative if
could be any integer (even negative if  ) so there are an infinite amount of possible values for
) so there are an infinite amount of possible values for 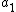 . She knows that
. She knows that  always decreases by 3 so if
always decreases by 3 so if  was divisible by
was divisible by  she could conclude
she could conclude  but because it's prime she can't even conclude that and so she didn't win any information.
but because it's prime she can't even conclude that and so she didn't win any information.
Python example
The following Python implementation of Shamir's Secret Sharing is
released into the Public Domain under the terms of CC0 and OWFa:
https://creativecommons.org/publicdomain/zero/1.0/
http://www.openwebfoundation.org/legal/the-owf-1-0-agreements/owfa-1-0
See the bottom few lines for usage. Tested on Python 2 and 3.
from __future__ import division
from __future__ import print_function
import random
import functools
- 12th Mersenne Prime
- (for this application we want a known prime number as close as
- possible to our security level; e.g. desired security level of 128
- bits -- too large and all the ciphertext is large; too small and
- security is compromised)
_PRIME = 2**127 - 1
- 13th Mersenne Prime is 2**521 - 1
_RINT = functools.partial(random.SystemRandom().randint, 0)
def _eval_at(poly, x, prime):
'''evaluates polynomial (coefficient tuple) at x, used to generate a shamir pool in make_random_shares below. ''' accum = 0 for coeff in reversed(poly): accum *= x accum += coeff accum %= prime return accum
def make_random_shares(minimum, shares, prime=_PRIME):
''' Generates a random shamir pool, returns the secret and the share points. ''' if minimum > shares: raise ValueError("pool secret would be irrecoverable") poly = [_RINT(prime) for i in range(minimum)] points = [(i, _eval_at(poly, i, prime)) for i in range(1, shares + 1)] return poly[0], pointsdef _extended_gcd(a, b):
''' division in integers modulus p means finding the inverse of the denominator modulo p and then multiplying the numerator by this inverse (Note: inverse of A is B such that A*B % p == 1) this can be computed via extended Euclidean algorithm http://en.wikipedia.org/wiki/Modular_multiplicative_inverse#Computation ''' x = 0 last_x = 1 y = 1 last_y = 0 while b != 0: quot = a // b a, b = b, a%b x, last_x = last_x - quot * x, x y, last_y = last_y - quot * y, y return last_x, last_y
def _divmod(num, den, p):
To explain what this means, the return value will be such that the following is true: den * _divmod(num, den, p) % p == num ''' inv, _ = _extended_gcd(den, p) return num * inv
def _lagrange_interpolate(x, x_s, y_s, p):
''' Find the y-value for the given x, given n (x, y) points; k points will define a polynomial of up to kth order ''' k = len(x_s) assert k == len(set(x_s)), "points must be distinct" def PI(vals): # upper-case PI -- product of inputs accum = 1 for v in vals: accum *= v return accum nums = [] # avoid inexact division dens = [] for i in range(k): others = list(x_s) cur = others.pop(i) nums.append(PI(x - o for o in others)) dens.append(PI(cur - o for o in others)) den = PI(dens) num = sum([_divmod(nums[i] * den * y_s[i] % p, dens[i], p) for i in range(k)]) return (_divmod(num, den, p) + p) % p
def recover_secret(shares, prime=_PRIME):
''' Recover the secret from share points (x,y points on the polynomial) ''' if len(shares) < 2: raise ValueError("need at least two shares") x_s, y_s = zip(*shares) return _lagrange_interpolate(0, x_s, y_s, prime)def main():
'''main function''' secret, shares = make_random_shares(minimum=3, shares=6)
print('secret: ', secret) print('shares:') if shares: for share in shares: print(' ', share) print('secret recovered from minimum subset of shares: ', recover_secret(shares[:3])) print('secret recovered from a different minimum subset of shares: ', recover_secret(shares[-3:]))if __name__ == '__main__':
Properties
Some of the useful properties of Shamir's  threshold scheme are:
threshold scheme are:
- Secure: Information theoretic security.
- Minimal: The size of each piece does not exceed the size of the original data.
- Extensible: When
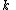 is kept fixed,
is kept fixed,  pieces can be dynamically added or deleted without affecting the other pieces.
pieces can be dynamically added or deleted without affecting the other pieces. - Dynamic: Security can be easily enhanced without changing the secret, but by changing the polynomial occasionally (keeping the same free term) and constructing new shares to the participants.
- Flexible: In organizations where hierarchy is important, we can supply each participant different number of pieces according to their importance inside the organization. For instance, the president can unlock the safe alone, whereas 3 secretaries are required together to unlock it.
A known issue in Shamir's Secret Sharing scheme is the verification of correctness of the retrieved shares during the reconstruction process, which is known as verifiable secret sharing. Verifiable secret sharing aims at verifying that shareholders are honest and not submitting fake shares.
See also
- Secret sharing
- Lagrange polynomial
- Homomorphic secret sharing - A simplistic decentralized voting protocol.
- Two-man rule
- Partial Password
References
- {{citation
| last = Shamir
| first = Adi
| authorlink = Adi Shamir
| title = How to share a secret
| journal = Communications of the ACM
| volume = 22
| issue = 11
| pages = 612–613
| doi = 10.1145/359168.359176
| year = 1979}}.
- {{citation|last=Liu|first=C. L.|authorlink=Chung Laung Liu|title=Introduction to Combinatorial Mathematics|publisher=McGraw-Hill|location=New York|year=1968}}.
- {{citation|last1=Dawson|first1=E.|last2=Donovan|first2=D.|year=1994|title=The breadth of Shamir's secret-sharing scheme|journal=Computers & Security|volume=13|pages=69–78|doi=10.1016/0167-4048(94)90097-3}}.
- {{citation|last=Knuth|first=D. E.|authorlink=Donald Knuth|year=1997|title=The Art of Computer Programming|edition=3rd|volume=II: Seminumerical Algorithms|page=505|publisher=Addison-Wesley}}.
- {{citation|last=Benzekki|first=K.|title= A Verifiable Secret Sharing Approach for Secure MultiCloud Storage|publisher=Springer|journal=In Ubiquitous Networking|location=Casablanca|volume=10542|year=2017}}.
- Changing Breeds (World of Darkness)
- Changing Faces (group)
- Changing Focus
- Changing Lanes
- Changing Man
- Changing New York
- Changing Partners
- Changing Places
- Changing room
- Changing room (disambiguation)
- Changing rooms
- Changing Rooms
- Changing table
- Changing the world without taking power
- Changi prison
- Changi Prison
- Changi Village
- Ch'ang-I Wang Ho
- Changji
- Changjiang (disambiguation)
- Chang Jiang River
- Changjiang River
- Changjie
- Changkufeng incident
- Chang Kuo-Jung