函数hanshu

数学中最重要的概念之一.它是从大量实际问题中抽象出来的，体现出合乎形式逻辑和辩证逻辑的数学思维.函数概念多方面地促使数学向前发展，它几乎是现代数学每一分支的主要研究对象.由于函数概念的内涵逐步扩充，因而数学新的分支也不断地涌现.
中学数学中函数的定义是：如果在某变化过程中有两个变量x和y，并且对于x在某个范围内的每一个确定的值，按照某个对应法则，y都有唯一确定的值和它对应，那么y就是x的函数，x叫做自变量，x的取值范围叫做函数的定义域.和x的值对应的y的值叫做函数值，函数值的集合叫做函数的值域.
从映射的观点给出函数的定义是：当集合A,B都是非空的数的集合，且B的每一个元素都有原象时，这样的映射f:A→B就是定义域A到值域B上的函数.函数是由定义域、值域以及定义域到值域上的对应法则三部分组成的一类特殊的映射.
例如函数y=x²+2，它的定义域是A={x|x∈R}，值域是B={y|y≥2}，对应法则是“平方加2”，这个函数就是一个集合A到B上的映射.
函数这个名词，是微积分的奠基人之一——德国的哲学家兼数学家G.W.莱布尼兹首先采用的.他用函数表示任何一个随着曲线上的点的变动而变动的量.与此同时，瑞士数学家雅克·贝努利给出了和G.
W.莱布尼兹相同的函数定义.1718年雅克·贝努利的弟弟约翰·贝努利给出了函数的如下定义：由任一变数和常数的任意形式所构成的量叫做这一变数的函数.后来约翰·贝努利的学生欧拉把函数定义又推进了一步，使之更加明朗化.他把凡是可以给出“解析式表示”的，通称为函数.这里的“解析式”包括多项式、对数式，三角式乃至幂级数.并且于1734年采用了现在通用的记号f(x)来表示函数.后来，由于对于一个函数表达方式是否唯一的问题，在不断的争议中逐渐澄清，法国数学家柯西又引入了新的函数定义：在某些变数间存在着一定的关系，当一经给定其中某一变数的值，其他变数的值也可随之而确定时，则将最初的变数称之为“自变数”，其他各变数则称为“函数”.到了19世纪德国数学家黎曼给出了函数的下述定义：对于x的每一个值，y总有完全确定的值与之对应，而不拘建立x,y之间的对应方法如何，均将y称为x的函数.另一个德国数学家狄利克雷也于1837年给出一个新的函数定义：对a≤x≤b之间的每一个x值，y总有完全确定的值与之对应，不论这一对应是用什么方法建立的，总可以把y称为x的函数.这两个定义都彻底抛弃了以前定义中解析式的束缚，特别突出了函数概念的本质——对应思想.例如当时出现的一些函数
y=〔x〕 (〔x〕≤x的最大整数)

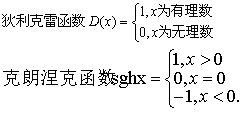
这些函数都极难用简单的包含自变量x的解析式表达，但它们都能表达一种规则，它们在研究函数过程中起着一定的作用.
这以后，逐渐将函数概念抽象化.对于y=f(x),x∈X,y∈Y.其中X,Y都是实数集或它的子集，函数f包含着两个内容：其一，通过f把X变到Y里面去，即f∶X→Y；其二，每一个x∈X，在f的作用下对应着f(x)，即x→f(x).这里f可以是数量间的运算关系，可以是极限运算，或其他运算，也可以是数学上某种约定.
函数概念的进一步发展，是放宽自变量的条件.与集合论的发展相互配合，函数概念打破了实数集合的限制，将X,Y从实数集合改变为一般集合，用“映射”观点建立函数概念.即若X,Y是两个非空集合，对于y=f(x),x∈X,y∈Y中的函数f包含着两个内容：其一，通过f把X映射到Y里面去，即f∶X→Y；其二，每一个x∈X在f的作用下对应着f(x).即x→f(x),f(x)是在映射f的作用下x的象，而x是f(x)的一个原象.
选择不同的X,Y集合，就能得到各类函数.如多元函数、复变函数、参数表达的函数等等.
进入20世纪以后，人们对于函数概念的认识继续深化，进入现代函数定义阶段，综上所述，可以看出函数概念在长期实践中日渐完善，并对数学的发展起着重要作用.