利用移轴化简方程liyong yizhou huajian fangcheng

❶公式法 把移轴公式代入已知的方程F(x,y)=0中，得新方程f(x′,y′)=0，然后适当地选择h,k的值，可以使方程化简.
在没有xy项的二次方程Ax²+Cy²+Dx+Ey+F=0中，通过移轴可以使方程化简.如果A,C都不为零，那么移轴后可以消去一次项，得到一个新方程（有心圆锥曲线的标准型方程），它的曲线对称于新坐标轴，也对称于新原点.如果A,C有且只有一个为零，那么移轴后可以消去y′的一次项系数或x′的一次项系数及常数项.得到一个新方程（无心圆锥曲线即抛物线的标准型方程），它的曲线对称于X′轴或Y′轴，顶点在新原点.
在只有xy的二次项的二次方程Bxy+Dx+Ey+F=0中，通过移轴可以消去它的一次项，得到形如x′y′=k的新方程，方程的曲线很容易作出.

❷配方法 对于缺少xy项的二元二次方程，可以用配平方法来确定h,k的值，达到化简方程的目的，这种方法常比代公式的方法来得简便.当二次方程Ax²+Cy²+Dx+Ey+F=0中A,C都不等于零时，令x′=x+D/2A,=y+E/2C，即可把方程化简：当A,C中有一个是0.(假定A=0,C≠0)时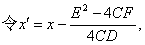，y’=y+E/2C(D≠0，否则为一元方程)即可把方程化简.