“Thaine's theorem”的意思、由来-开放百科全书

词条

Thaine's theorem

释义

Formulation
References

In mathematics, Thaine's theorem is an analogue of Stickelberger's theorem for real abelian fields, introduced by {{harvs|txt|last=Thaine|year=1988}}. Thaine's method has been used to shorten the proof of the Mazur–Wiles theorem {{harv|Washington|1997}}, to prove that some Tate–Shafarevich groups are finite, and in the proof of Mihăilescu's theorem {{harv|Schoof|2008}}.

Formulation

Let and be distinct odd primes with not dividing . Let 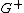be the Galois group of 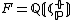over , let be its group of units, let be the subgroup of cyclotomic units, and let 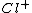be its class group. If 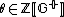annihilates 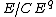then it annihilates .

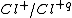References

{{citation|mr=2459823

|last=Schoof|first= René|authorlink=René Schoof
|title=Catalan's conjecture
|series=Universitext|publisher= Springer-Verlag London, Ltd.|place= London|year= 2008|isbn= 978-1-84800-184-8 }} See in particular Chapter 14 (pp. 91–94) for the use of Thaine's theorem to prove Mihăilescu's theorem, and Chapter 16 "Thaine's Theorem" (pp. 107–115) for proof of a special case of Thaine's theorem.

{{citation|mr=0951505

|last=Thaine |first=Francisco
|title=On the ideal class groups of real abelian number fields
|journal=Annals of Mathematics|series=2nd ser. |volume=128 |year=1988|issue= 1|pages= 1–18|jstor=1971460 |doi=10.2307/1971460}}

{{citation|first=Lawrence C.|last= Washington|authorlink=Lawrence C. Washington

|title=Introduction to Cyclotomic Fields|series=Graduate Texts in Mathematics|volume= 83|publisher=Springer-Verlag|place= New York|year= 1997|edition=2nd|isbn=0-387-94762-0 |mr=1421575}} See in particular Chapter 15 ([https://books.google.com/books?id=qea_OXafBFoC&pg=PA332 pp. 332–372]) for Thaine's theorem (section 15.2) and its application to the Mazur–Wiles theorem.

2 : Cyclotomic fields|Theorems in algebraic number theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。