塞瓦定理saiwa dingli

若X,Y,Z分别是△ABC三边BC,CA,AB或其延长线上的点.则AX,BY,CZ三线共点或互相平行的充分必要条件是

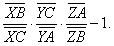
必要性：若AX∥BY∥CZ(如图1)，显然

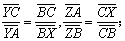
所以

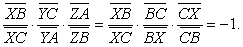
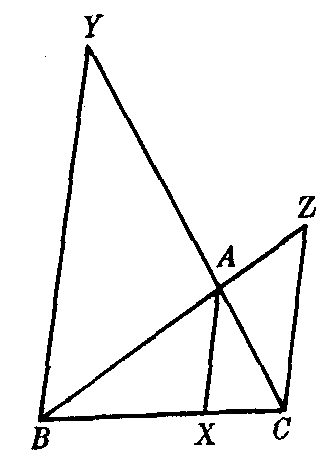
图1

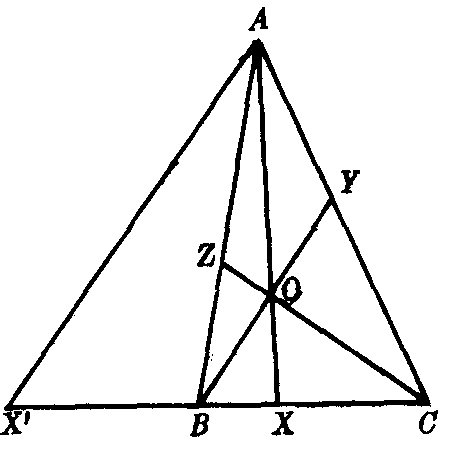
图2

若AX,BY,CZ交于一点O(如图2)，因为BOY是△AXC的截线，由梅内劳斯定理得：

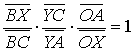
同理，

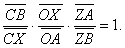
相乘，并注意有向线段的符号，化简可得：

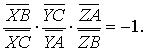
充分性： 若

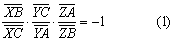
当BY∥CZ时，如图，作AX′∥BY交BC于X′，当BY交CZ于O时，连AO直线，必交BC于X′(这是

因为若AO∥BC，则

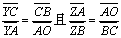
代入(1)式，得

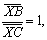
矛盾).

因此有

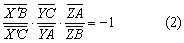
比较(1)、(2)得

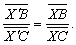
因此，X′与X重合，所以AX,BY,XZ三线共点或互相平行.
塞瓦定理可用来证明三线共点问题.