数列的极限shulie de jixian
是描述当n无限变大时数列{an}的变化趋势的重要概念.
对于数列{an},如果存在常数a,使得当n无限增大时an能无限地接近a,就说a是数列{an}的极限.例如,数列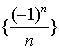 的极限为0;数列
的极限为0;数列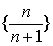 的极限为1;常数列{2}的极限为2;数列{(-1)n}不存在极限。
的极限为1;常数列{2}的极限为2;数列{(-1)n}不存在极限。
严格地说,设{an}是一个数列,a是一个常数,如果对于任意给定的正数ε,都存在某一个自然数N,使得当n>N时,总有
|an -a|<ε
则称数列 {an} 存在极限,且极限为a,或称数列{an} 收敛于a, 并记作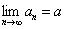 或a n→a (n→∞)。
或a n→a (n→∞)。若数列 {an} 不存在极限,则称数列 {an} 发散。数列 {an}以a为极限的直观说法是,对于任意给定的一个小正数ε,要使|an-a|小于这个ε,只要n.充分大以后就能实现。
数列{an}以常数a为极限的几何意义是,对于点a的任何一个ε邻域(a-ε,a+ε),总有某个序号N,使数列 (an}在aN以后的所有的点aN+1,aN+2,…都落在这个邻域内,而至多只有N个点a1,a2,…,aN落在这个邻域以外 (见下图)。
![]()